计算图详解(静态计算图和动态计算图)
计算图(Compute Graph)是张量程序抽象的一种具体形式,以特殊的有向无环图(DAG)形式,表征了从输入到输出的计算流程。
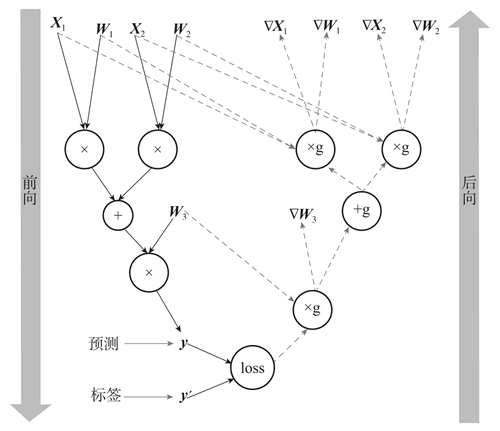
图 1 计算图的架构
如上图所示,计算图由两部分构成:张量和算子。其中,张量是多维数组,用于存储数据,而算子则定义了如何对这些数据进行处理。在深度学习框架(如TensorFlow或PyTorch)中,计算图是构建、理解、优化神经网络模型的基础。
每个算子执行特定的计算任务,如加法、乘法或卷积,并输出一个新的张量。模型的整个计算过程被模块化为不同的操作单元,每个单元执行明确的函数。自动微分机制利用这种结构,在训练期间通过后向传播算法高效地计算梯度。这些梯度对于通过梯度下降法优化模型的权重参数至关重要。
除了自动微分外,计算图还能优化整个计算流程。例如,框架可以识别并消除重复的计算,或者重新安排操作的顺序来提升计算效率。通过这种方式,开发者可以更加高效地实现模型训练和推理,尤其在处理复杂的神经网络结构时更是如此。
在计算图中,张量构成了数据的基本单元,贯穿于整个计算过程,包含输入数据、模型参数及其生成的中间结果。从数学角度来看,张量是标量和向量的高维推广,本质上是一个多维数组。
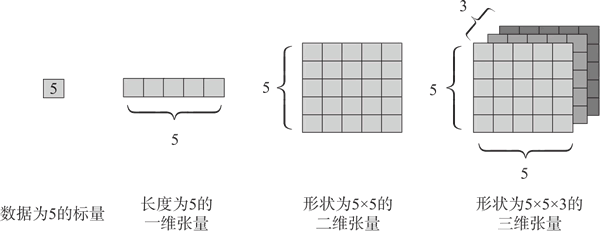
图 2 张量可视化
如上图所示,张量可能是零维的,代表一个单一数值(标量),也可能是一维的(向量)、二维的(矩阵)或者是更高维度的数组形态。
例如,一个三维张量可以用于存储彩色图像的像素值,其中两维对应于图像的高度和宽度,第三维则对应于颜色通道。在深度学习的背景下,模型的参数(比如权重矩阵和偏差向量)是在学习过程中不断优化的变量。这些参数张量在神经网络的各层中发挥作用,通过学习数据中的模式来调整其值。
当数据在模型各层之间传递时,每一层都会使用其参数张量处理数据,生成新的中间结果张量。这一过程是模型学习的基础,它允许模型在层之间传递信息,并逐渐提取出更高层次的特征。
此外,计算图在训练阶段还会产生梯度张量,这是模型损失相对于每个参数变化的度量。梯度张量与参数张量具有相同的形状,为参数更新提供了必要的信息,以便降低整体的损失函数值。
在计算图中,算子定义了神经网络中张量如何被处理与转换。这些算子规定了数据在神经网络的各个节点间的流动路径,包括权重加总、激活函数调用和卷积等多种操作。
根据其功能,算子可归类为张量操作算子、神经网络算子、数据流算子及控制流算子:
1) 张量操作算子涉及结构性变换与数学运算。其中,结构操作算子负责调整张量的维度和形状,例如在图像处理中,它们可以改变图像张量的通道排列次序。数学运算类算子执行诸如矩阵乘法和范数计算等基本数学操作,这些运算构成了神经网络梯度计算和参数优化的基础。
2) 神经网络算子负责特征提取、激活函数和损失计算。特征提取算子(如卷积)用于从输入数据中提取关键特征;激活函数(如 ReLU 或 Sigmoid)引入非线性以增强模型对复杂数据模式的捕捉能力;损失函数和优化算子则直接关联至模型参数的更新,影响训练效率。
3) 数据流算子负责数据预处理和优化数据读取过程。预处理操作(如图像裁剪、填充和归一化)旨在提升模型的训练效率和泛化能力;数据载入算子通过批处理和预加载等技术,优化数据的输入流。
4) 控制流算子在计算图中控制数据的流动路径,通过条件语句和循环实现模型的动态行为,对梯度的后向传播和计算效率有直接影响。
在深度学习模型的训练阶段,每个算子按照预定义的规则处理输入张量,并生成输出张量,传递至下一节点。这个过程从输入层展开至输出层。在后向传播过程中,导数(梯度)自输出层向输入层传播,依据链式法则计算每个参数的梯度,用于模型参数的更新。
计算图不仅清晰地展示了模型的构成,还在模型的训练和推理过程中为优化提供了框架。通过挖掘计算图的结构信息,可实施各种优化策略,提升模型的计算效率与性能。
计算图分为静态计算图和动态计算图两大类。
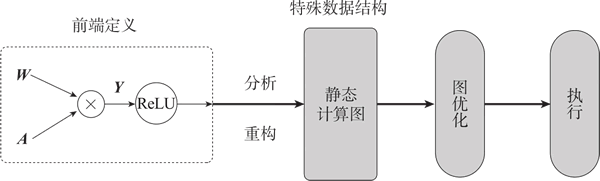
图 3 静态计算图生成与执行
如上图所示,在模型构建阶段,开发者使用 Python 等前端语言来规划模型架构,定义各层及其算子。这个阶段完成后,就像在编程中的编译步骤一样,生成了一个完整且优化的计算图。当进入执行阶段,这个计算图不再依赖前端语言的解释或编译,而是可以直接在硬件上执行,有效提升了执行效率。
以 TensorFlow 1.x 为例,静态计算图的创建涉及定义占位符、模型参数、结构、损失函数和优化策略等步骤。如下所示的代码片段展示了一个线性模型的构建过程。
静态计算图的结构预先确定且不变,减少了运行时的额外开销,便于跨平台运行和部署,同时允许模型的序列化和保存,推理时无须重新编译。
然而,静态计算图一旦构建完毕,就无法修改其结构。这在进行模型调试时可能引入挑战,因为优化和转换后的计算图可能与开发者编写的原始代码有显著差异,错误追踪可能会指向经过优化的代码而非源代码,给定位问题带来难度。此外,定义复杂网络结构和训练过程的代码可能比较烦琐,需要开发者有较高的技术水平。
动态计算图采用命令式编程范式,这意味着编程语言中的命令会按照它们在代码中的顺序立即执行。这种特性使得动态计算图在模型构建和实验阶段非常灵活,允许研究人员频繁修改模型和尝试新的想法。此外,由于其即时执行的特性,动态计算图在调试过程中更为直观,用户可以随时检查和打印模型的状态。
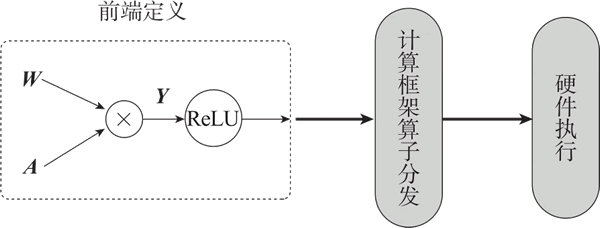
图 4 动态计算图的生成与执行
如上图所示,动态计算图依靠编程语言的解释器在运行时解析代码,并通过机器学习框架的算子分发机制,根据输入数据的特性和运算环境,动态选用最适宜的算子进行计算。这种方法的一个明显优势是提高了调试过程的透明度,编程人员可以随时检查模型内部的状态。例如,在动态计算图框架(如PyTorch)中,模型和计算图的构建是交织在一起的。
如下所示的代码展示了一个与图 4 中 TensorFlow 1.x 功能相同的线性模型。
开发者可以使用普通的控制流(如循环和条件语句),而模型的每一次执行都可以是不同的。这种即时的反馈和灵活性是动态计算图的显著特点。与之相反,静态计算图的执行效率通常更高,但在构建和调试过程中不如动态计算图直观和灵活。
动态计算图和静态计算图的主要区别在于它们各自的编译和执行方式。虽然静态计算图在运行时性能上可能更具优势,动态计算图则在开发和调试过程中为用户提供了更为丰富的直观体验和便利。在选择使用哪种类型的图时,研究人员需要根据具体任务的需求和偏好做出决定。
静态计算图和动态计算图的对比如下表所示。
为了结合动态计算图的易用性和静态计算图的高效性,主流框架提供了从动态计算图到静态计算图的转换技术。TensorFlow 通过 @tf_function 和 AutoGraph 机制实现转换,而 PyTorch 则通过 torch.jit.script() 和 torch.jit.trace() 提供类似功能。这些方法允许开发者在动态计算图模式下进行开发和调试,然后转换为静态计算图以提高执行效率。
各主流框架支持的动态计算图转静态计算图的技术如下表所示。
PyTorch 的 torch.jit.trace() 函数实现了一种基于追踪的转换方法。在这个过程中,模型首先在动态计算图模式下执行。执行时,框架记录下被调度的算子及其执行顺序,并据此构建出一个静态计算图模型,这个模型随后可以被保存和重新加载。
然而,这种基于追踪的方法存在局限性,若模型中包含数据依赖的条件分支,追踪过程仅能捕捉到实际执行路径上的分支,这可能导致某些条件分支被遗漏,从而生成一个不完整的静态计算图。
而 PyTorch 的 torch.jit.script() 函数采用基于源码的转换策略。此方法通过对模型代码进行深入分析,识别并映射出动态计算图中的控制流结构,自动将动态计算图代码转写为适合静态计算图执行的代码。这一过程包括对代码的词法和语法分析,并且要求预设的转换器理解动态计算图的语义,转换为静态计算图的表达。这种方法在处理包含复杂控制流的模型时更为精确和健壮,尽管其实现更为复杂。
动静态图的转换技术为开发者提供了前所未有的灵活性。在模型开发和调试的初期阶段,可以充分利用动态计算图的优势;而在模型部署阶段,为了优化性能,可以将模型转换为静态计算图。这不仅提高了执行效率,而且由于静态计算图模型的跨平台兼容性,大大简化了模型在不同硬件设备上的部署过程。

图 1 计算图的架构
如上图所示,计算图由两部分构成:张量和算子。其中,张量是多维数组,用于存储数据,而算子则定义了如何对这些数据进行处理。在深度学习框架(如TensorFlow或PyTorch)中,计算图是构建、理解、优化神经网络模型的基础。
每个算子执行特定的计算任务,如加法、乘法或卷积,并输出一个新的张量。模型的整个计算过程被模块化为不同的操作单元,每个单元执行明确的函数。自动微分机制利用这种结构,在训练期间通过后向传播算法高效地计算梯度。这些梯度对于通过梯度下降法优化模型的权重参数至关重要。
除了自动微分外,计算图还能优化整个计算流程。例如,框架可以识别并消除重复的计算,或者重新安排操作的顺序来提升计算效率。通过这种方式,开发者可以更加高效地实现模型训练和推理,尤其在处理复杂的神经网络结构时更是如此。
在计算图中,张量构成了数据的基本单元,贯穿于整个计算过程,包含输入数据、模型参数及其生成的中间结果。从数学角度来看,张量是标量和向量的高维推广,本质上是一个多维数组。

图 2 张量可视化
如上图所示,张量可能是零维的,代表一个单一数值(标量),也可能是一维的(向量)、二维的(矩阵)或者是更高维度的数组形态。
例如,一个三维张量可以用于存储彩色图像的像素值,其中两维对应于图像的高度和宽度,第三维则对应于颜色通道。在深度学习的背景下,模型的参数(比如权重矩阵和偏差向量)是在学习过程中不断优化的变量。这些参数张量在神经网络的各层中发挥作用,通过学习数据中的模式来调整其值。
当数据在模型各层之间传递时,每一层都会使用其参数张量处理数据,生成新的中间结果张量。这一过程是模型学习的基础,它允许模型在层之间传递信息,并逐渐提取出更高层次的特征。
此外,计算图在训练阶段还会产生梯度张量,这是模型损失相对于每个参数变化的度量。梯度张量与参数张量具有相同的形状,为参数更新提供了必要的信息,以便降低整体的损失函数值。
在计算图中,算子定义了神经网络中张量如何被处理与转换。这些算子规定了数据在神经网络的各个节点间的流动路径,包括权重加总、激活函数调用和卷积等多种操作。
根据其功能,算子可归类为张量操作算子、神经网络算子、数据流算子及控制流算子:
1) 张量操作算子涉及结构性变换与数学运算。其中,结构操作算子负责调整张量的维度和形状,例如在图像处理中,它们可以改变图像张量的通道排列次序。数学运算类算子执行诸如矩阵乘法和范数计算等基本数学操作,这些运算构成了神经网络梯度计算和参数优化的基础。
2) 神经网络算子负责特征提取、激活函数和损失计算。特征提取算子(如卷积)用于从输入数据中提取关键特征;激活函数(如 ReLU 或 Sigmoid)引入非线性以增强模型对复杂数据模式的捕捉能力;损失函数和优化算子则直接关联至模型参数的更新,影响训练效率。
3) 数据流算子负责数据预处理和优化数据读取过程。预处理操作(如图像裁剪、填充和归一化)旨在提升模型的训练效率和泛化能力;数据载入算子通过批处理和预加载等技术,优化数据的输入流。
4) 控制流算子在计算图中控制数据的流动路径,通过条件语句和循环实现模型的动态行为,对梯度的后向传播和计算效率有直接影响。
在深度学习模型的训练阶段,每个算子按照预定义的规则处理输入张量,并生成输出张量,传递至下一节点。这个过程从输入层展开至输出层。在后向传播过程中,导数(梯度)自输出层向输入层传播,依据链式法则计算每个参数的梯度,用于模型参数的更新。
计算图不仅清晰地展示了模型的构成,还在模型的训练和推理过程中为优化提供了框架。通过挖掘计算图的结构信息,可实施各种优化策略,提升模型的计算效率与性能。
计算图分为静态计算图和动态计算图两大类。
静态计算图
静态计算图是在模型执行之前完整定义的图,其结构以及其中的算子和张量流动都在实际进行任何计算之前已被设定,遵循“编译后执行”的原则,从而分离了计算图的定义与执行过程。
图 3 静态计算图生成与执行
如上图所示,在模型构建阶段,开发者使用 Python 等前端语言来规划模型架构,定义各层及其算子。这个阶段完成后,就像在编程中的编译步骤一样,生成了一个完整且优化的计算图。当进入执行阶段,这个计算图不再依赖前端语言的解释或编译,而是可以直接在硬件上执行,有效提升了执行效率。
以 TensorFlow 1.x 为例,静态计算图的创建涉及定义占位符、模型参数、结构、损失函数和优化策略等步骤。如下所示的代码片段展示了一个线性模型的构建过程。
import tensorflow as tf
# 定义输入和模型参数
x = tf.placeholder(tf.float32, shape=(None, 3))
y = tf.placeholder(tf.float32, shape=(None, 1))
W = tf.Variable(tf.random_normal([3, 1]), name="weights")
b = tf.Variable(tf.zeros([1]), name="bias")
# 构建线性模型
pred = tf.matmul(x, W) + b
# 定义损失函数和梯度下降优化器
loss = tf.reduce_mean(tf.square(pred - y))
optimizer = tf.train.GradientDescentOptimizer(0.01).minimize(loss)
# 执行计算图
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(1000):
batch_x, batch_y = ... # 获取数据
_, 1 = sess.run([optimizer, loss], feed_dict={x: batch_x, y: batch_y})
静态计算图在编译时能获得整个模型的全局信息,这允许框架在模型运行前对整个图进行深入的优化,如算子融合、内存优化、确定执行路径等。这些优化能够显著提升大规模、复杂网络的计算效率。静态计算图的结构预先确定且不变,减少了运行时的额外开销,便于跨平台运行和部署,同时允许模型的序列化和保存,推理时无须重新编译。
然而,静态计算图一旦构建完毕,就无法修改其结构。这在进行模型调试时可能引入挑战,因为优化和转换后的计算图可能与开发者编写的原始代码有显著差异,错误追踪可能会指向经过优化的代码而非源代码,给定位问题带来难度。此外,定义复杂网络结构和训练过程的代码可能比较烦琐,需要开发者有较高的技术水平。
动态计算图
与静态计算图不同,动态计算图在模型运行时,每执行一个操作,都会立即被计算并返回结果,而不是先构建一个完整的计算图再执行。这种方式也被称为“即时执行”或“命令式执行”。动态计算图采用命令式编程范式,这意味着编程语言中的命令会按照它们在代码中的顺序立即执行。这种特性使得动态计算图在模型构建和实验阶段非常灵活,允许研究人员频繁修改模型和尝试新的想法。此外,由于其即时执行的特性,动态计算图在调试过程中更为直观,用户可以随时检查和打印模型的状态。

图 4 动态计算图的生成与执行
如上图所示,动态计算图依靠编程语言的解释器在运行时解析代码,并通过机器学习框架的算子分发机制,根据输入数据的特性和运算环境,动态选用最适宜的算子进行计算。这种方法的一个明显优势是提高了调试过程的透明度,编程人员可以随时检查模型内部的状态。例如,在动态计算图框架(如PyTorch)中,模型和计算图的构建是交织在一起的。
如下所示的代码展示了一个与图 4 中 TensorFlow 1.x 功能相同的线性模型。
import torch
import torch.optim as optim
# 定义模型参数
W = torch.randn(3, 1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# 定义线性模型函数
def linear_model(x):
return x @ W + b
# 定义损失函数
def mse_loss(pred, y):
return ((pred - y) ** 2).mean()
# 定义优化器
optimizer = optim.SGD([W, b], lr=0.01)
# 运行模型训练
for i in range(1000):
batch_x, batch_y = ... # 获取数据
optimizer.zero_grad() # 梯度清零
pred = linear_model(batch_x)
loss = mse_loss(pred, batch_y)
loss.backward() # 后向传播计算梯度
optimizer.step() # 更新参数
在这个 PyTorch 的例子中,模型的计算图在每次迭代时都是动态创建的。requires_grad=True 告诉 PyTorch 跟踪这些张量上的所有操作,以便在后向传播时自动计算梯度。这个过程与 TensorFlow 静态计算图的主要区别在于计算图的动态性,模型定义更接近于正常的 Python 代码。开发者可以使用普通的控制流(如循环和条件语句),而模型的每一次执行都可以是不同的。这种即时的反馈和灵活性是动态计算图的显著特点。与之相反,静态计算图的执行效率通常更高,但在构建和调试过程中不如动态计算图直观和灵活。
动态计算图和静态计算图的主要区别在于它们各自的编译和执行方式。虽然静态计算图在运行时性能上可能更具优势,动态计算图则在开发和调试过程中为用户提供了更为丰富的直观体验和便利。在选择使用哪种类型的图时,研究人员需要根据具体任务的需求和偏好做出决定。
静态计算图和动态计算图的对比如下表所示。
| 特性 | 静态计算图 | 动态计算图 |
|---|---|---|
| 即时获取中间结果 | 否 | 是 |
| 代码调试难易 | 难 | 易 |
| 控制流实现方式 | 特定的语法 | 前端语言语法 |
| 性能 | 优化策略多,性能更佳 | 图优化受限,性能较差 |
| 内存占用 | 内存占用少 | 内存占用相对较多 |
| 模型部署 | 可直接部署 | 不可直接部署 |
为了结合动态计算图的易用性和静态计算图的高效性,主流框架提供了从动态计算图到静态计算图的转换技术。TensorFlow 通过 @tf_function 和 AutoGraph 机制实现转换,而 PyTorch 则通过 torch.jit.script() 和 torch.jit.trace() 提供类似功能。这些方法允许开发者在动态计算图模式下进行开发和调试,然后转换为静态计算图以提高执行效率。
各主流框架支持的动态计算图转静态计算图的技术如下表所示。
| 框架 | 动态计算图转静态计算图 |
|---|---|
| TensorFlow | 使用 @tf_function 追踪算子调度以构建静态计算图,其中 AutoGraph 机制可以自动将控制流转换为静态表示 |
| PyTorch |
torch.jit.trace() 支持基于追踪转换 torch.jit.script() 支持基于源码转换 |
PyTorch 的 torch.jit.trace() 函数实现了一种基于追踪的转换方法。在这个过程中,模型首先在动态计算图模式下执行。执行时,框架记录下被调度的算子及其执行顺序,并据此构建出一个静态计算图模型,这个模型随后可以被保存和重新加载。
然而,这种基于追踪的方法存在局限性,若模型中包含数据依赖的条件分支,追踪过程仅能捕捉到实际执行路径上的分支,这可能导致某些条件分支被遗漏,从而生成一个不完整的静态计算图。
而 PyTorch 的 torch.jit.script() 函数采用基于源码的转换策略。此方法通过对模型代码进行深入分析,识别并映射出动态计算图中的控制流结构,自动将动态计算图代码转写为适合静态计算图执行的代码。这一过程包括对代码的词法和语法分析,并且要求预设的转换器理解动态计算图的语义,转换为静态计算图的表达。这种方法在处理包含复杂控制流的模型时更为精确和健壮,尽管其实现更为复杂。
动静态图的转换技术为开发者提供了前所未有的灵活性。在模型开发和调试的初期阶段,可以充分利用动态计算图的优势;而在模型部署阶段,为了优化性能,可以将模型转换为静态计算图。这不仅提高了执行效率,而且由于静态计算图模型的跨平台兼容性,大大简化了模型在不同硬件设备上的部署过程。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: