数据清洗是什么,数据清洗详解(Python实现)
数据清洗的主要工作是删除原始数据集中的无关数据、重复数据,平滑噪声数据,筛选掉与挖掘主题无关的数据,处理缺失值、异常值等。
缺失值处理
删除记录、数据插补和不处理是处理缺失值的3种主要方法。其中,数据插补是使用最多的,数据插补包括均值/中位数/众数插补、固定值插补、近邻值插补、回归方法插补和插值法。1、拉格朗日插值法
拉格朗日插值法是一个数学问题。任给定 F 中 2n+2 个数 x1,x2,…,xn+1,y1,y2,…,yn+1,其中 x1,x2,…,xn+1 互不相同,则存在唯一的次数不超过 n 的多项式 pn(x),满足 pn(xi)=y1(i=1, 2, …, n+1),下面的式子: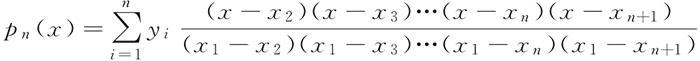
称作拉格朗日插值公式。
将缺失的函数值对应的点 x 代入插值公式即得到缺失值的近似值 L(x)。
但是当插值节点增减时,插值多项式就会随之变化,这在实际计算中是很不方便的,为了克服这一点,提出了牛顿插值法。
2、牛顿插值法
1) 差商公式
函数 f(x) 在两个互异点 xi、xj 处的 1 阶差商定义为: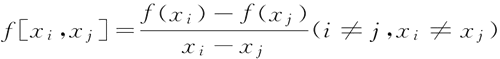
2 阶差商为:
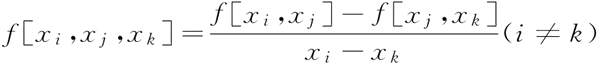
k+1 阶差商为:

2) 联立以上差商公式建立插值多项式
依次代入,可得牛顿差值公式: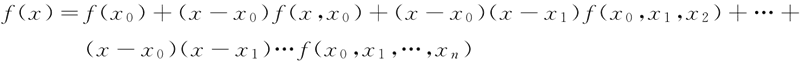
可记为:f(x)=Nn+Rn(x)。其中,Rn(x) 为牛顿差值公式的余项或截断误差,当 n 趋于无穷大时为零。
3) 将缺失的函数值对应的点x带入插值公式即得到缺失值的近似值 f(x)
牛顿插值法的优点是计算较简单,尤其是增加节点时,计算只增加一项,这是拉格朗日插值法无法比的。牛顿插值法的缺点是仍没有改变拉格朗日的插值曲线在节点处有尖点、不光滑、插值多项式在节点处不可导等。
【实例】用不同方法实现缺失值插补。
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
# 缺失值插补
# 均值/中位数/众数插补、临近值插补、插值法
# 分别求出均值/中位数/众数
u = s.mean() # 均值
me = s.median() # 中位数
mod = s.mode() # 众数
print('均值为:%.2f,中位数为:%.2f' % (u, me))
print('众数为:', mod.tolist())
# 用均值填补
s.fillna(u, inplace=True)
print('均值填补:', s)
# 用中位数填补
s.fillna(me, inplace=True)
print('中位数填补:', s)
# 用众数填补
s.fillna(mod, inplace=True)
print('众数填补:', s)
# 临近值填补,用前值插补
s.fillna(method='ffill', inplace=True)
from scipy.interpolate import lagrange
data = pd.Series(np.random.rand(100) * 100)
data[3, 6, 33, 56, 45, 66, 67, 80, 90] = np.nan
print('拉格朗日插值法:', data.head())
print('总数据量:%i' % len(data))
# 创建数据
data_na = data[data.isnull()]
print('缺失值数据量:%i' % len(data_na))
print('缺失数据占比:%.2f%%' % (len(data_na) / len(data) * 100))
# 缺失值的数量
data_c = data.fillna(data.median()) # 中位数填充缺失值
fig, axes = plt.subplots(1, 4, figsize=(20, 5))
data.plot.box(ax=axes[0], grid=True, title='数据分布')
data.plot(kind='kde', style='--r', ax=axes[1], grid=True, title='删除缺失值', xlim=[-50, 150])
data_c.plot(kind='kde', style='--b', ax=axes[2], grid=True, title='缺失值填充中位数', xlim=[-50, 150])
# 密度图查看缺失值情况
def na_c(s, n, k=5):
y = s[list(range(n - k, n + 1 + k))] # 取数
y = y[y.notnull()] # 剔除空值
return lagrange(y.index, list(y))(n)
# 创建函数,做插值,由于数据量原因,以空值前后5个数据(共10个数据)做插值
na_re = []
for i in range(len(data)):
if data.isnull()[i]:
data[i] = na_c(data, i)
print(na_c(data, i))
na_re.append(data[i])
data.dropna(inplace=True) # 清除插值后仍存在的缺失值
data.plot(kind='kde', style='--k', ax=axes[3], grid=True, title='拉格朗日插值后', xlim=[-50, 150])
运行程序,输出如下:
均值为:47.43,中位数为:47.43
众数为:[47.42857142857143]
均值填补:0 12.000000
1 33.000000
2 45.000000
...
8 47.428571
9 99.000000
dtype:float64
中位数填补:0 12.000000
1 33.000000
2 45.000000
...
8 47.428571
9 99.000000
dtype:float64
众数填补:0 12.000000
1 33.000000
2 45.000000
...
8 47.428571
9 99.000000
dtype:float64
拉格朗日插值法:0 38.195044
1 79.207828
2 40.205426
3 NaN
4 29.360929
dtype:float64
总数据量:100
缺失值数据量:9
缺失数据占比:9.00%
33.11088660504207
-25.547390080914283
96.58480834960938
111.20849609375
-18.59375
8.95098876953125
-38.6337890625
362.0
216.0
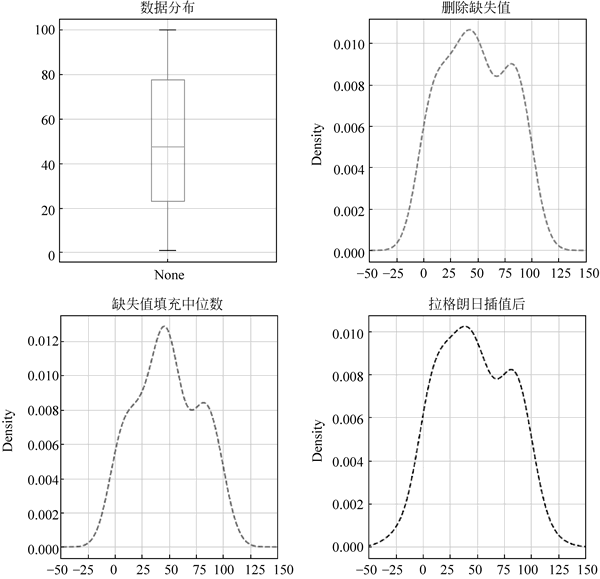
图 6 数据缺失值插补效果
异常值分析
异常值是指在数据集中存在的不合理的点(异常点),这些点如果不剔除或者不修正而错误地包括进数据的计算分析过程中,那么会对结果产生非常不好的影响,导致结果偏差(不准确)。因此,重视异常值的出现,分析其产生原因,并对异常值进行剔除或者修正就显得尤其重要。1、如何发现异常值
发现异常值的方法有很多种,例如,简单地确定某个指标的阈值,进行判断,也可以基于统计学方法,同时还有基于机器学习的离群点检测方法,本小节主要介绍统计学方法和机器学习方法。1) 3σ原则
在统计学中,如果一个数据分布近似正态,那么约有 68% 的数据值会在均值的一个标准差范围内,约有 95% 的数据值会在两个标准差范围内,约有 99.7% 的数据值会在三个标准差范围内。但是,当数据不服从正态分布时,可以通过远离平均距离多少倍的标准差来判定,多少倍的取值需要根据经验和实际情况来决定。【实例】利用 3σ 原则分析异常值。
import statsmodels as stats
# 3σ原则:如果数据服从正态分布,异常值被定义为一组测定值中与平均值的偏差超过3倍的值
# p(|x-μ| > 3σ) ≤ 0.003
data = pd.Series(np.random.randn(10000) * 100)
u = data.mean() # 计算均值
std = data.std() # 计算标准差
print('均值为:%.3f,标准差为:%.3f' % (u, std))
# 正态性检验
fig = plt.figure(figsize=(10, 6))
ax1 = fig.add_subplot(2, 1, 1)
# 绘制数据密度曲线
data.plot(kind='kde', grid=True, style='-k', title='密度曲线')
ax2 = fig.add_subplot(2, 1, 2)
error = data[np.abs(data - u) > 3 * std]
data_c = data[np.abs(data - u) <= 3 * std]
print("异常值共%d条" % len(error))
# 筛选出异常值error、剔除异常值之后的数据data_c
plt.scatter(data_c.index, data_c, color='k', marker='.', alpha=0.3)
plt.scatter(error.index, error, color='r', marker='.', alpha=0.5)
plt.xlim([-10, 10010])
plt.grid()
运行程序,输出如下:
均值为:-2.220,标准差为:100.897
异常值共29条
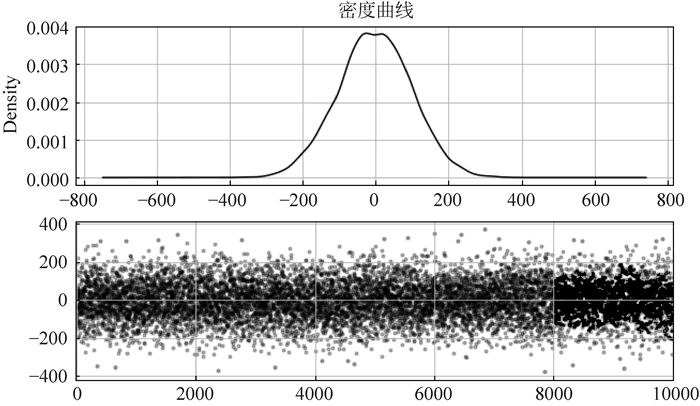
图 7 筛选出异常值效果
2) 箱形图
箱形图是通过数据集的四分位数形成的图形化描述,这是一种非常简单而且有效的可视化离群点的方法。如果把上下触须作为数据分布的边界,任何高于上触须或低于下触须的数据点都被认为是离群点或异常值。箱形图依据实际数据绘制,没有对数据做任何限制性要求,它只是真实直观地表现数据分布的本来面貌;另外,箱形图判断异常值的标准是以四分位数和四分位距为基础,四分位数具有一定的健壮性,多达 25% 的数据可以变得任意远,不会很大地扰动四分位数,所以异常值不能对这个标准加以影响。
由此可见,箱形图识别异常值的结果比较客观,在识别异常值方面有一定的优越性。
【实例】箱形图分析。
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10, 6))
ax1 = fig.add_subplot(2, 1, 1)
color = dict(boxes='DarkGreen', whiskers='DarkOrange', medians='DarkBlue', caps='Gray')
data.plot.box(vert=False, grid=True, color=color, ax=ax1, label='样本数据')
# 从箱形图观察数据分布情况,以内限为界
s = data.describe()
print('数据分布情况:', s)
# 基本统计量
q1 = s['25%']
q3 = s['75%']
iqr = q3 - q1
mi = q1 - 1.5 * iqr
ma = q3 + 1.5 * iqr
print('分位差为:%.3f,下限为:%.3f,上限为:%.3f' % (iqr, mi, ma))
# 计算分位差
ax2 = fig.add_subplot(2, 1, 2)
error = data[(data < mi) | (data > ma)]
data_c = data[(data >= mi) & (data <= ma)]
# 筛选出异常值error、剔除异常值之后的数据data_c
print('异常值共%i条' % len(error))
# 图表表达
plt.scatter(data_c.index, data_c, color='k', marker='.', alpha=0.3)
plt.scatter(error.index, error, color='r', marker='.', alpha=0.5)
plt.xlim([-10, 10010])
plt.grid()
运行程序,输出如下:
数据分布情况: count 10000.000000
mean 2.187945
std 99.159398
min -367.567507
25% -65.421817
50% 2.034342
75% 70.078261
max 359.725783
dtype: float64
分位差为: 135.500,下限为: -268.672,上限为: 273.328
异常值共56条
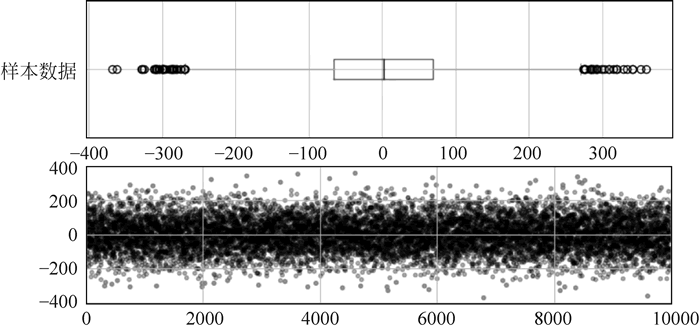
图 8 用箱形图分析异常值
3) DBSCAN算法
从基于密度(DBSCAN)的观点来说,离群点是在低密度区域中的对象。基于密度的离群点检测与基于邻近度的离群点检测密切相关,因为密度通常用邻近度定义,DBSCAN 就是一种使用密度的聚类算法。【实例】利用 DBSCAN 算法检测异常数据。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
# 生成随机簇类数据,样本数为600,类别为5
X, y = make_blobs(random_state=170,
n_samples=600,
centers=5)
# 绘制原始数据图
plt.scatter(X[:, 0], X[:, 1])
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()
# DBSCAN聚类算法,按照经验minPts=2 * ndims,因此设置min_samples=4
dbscan = DBSCAN(eps=1, min_samples=4)
clusters = dbscan.fit_predict(X)
# DBSCAN聚类结果可视化
plt.scatter(X[:, 0], X[:, 1],
c=clusters,
cmap="plasma")
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.title("eps=0.5, min_samples=4")
plt.show()
# 性能评价指标ARI
from sklearn.metrics.cluster import adjusted_rand_score
# ARI指数,ARI=0.99,为了减少算法的计算量,可以尝试减小min_samples的值
print("ARI=", round(adjusted_rand_score(y, clusters), 2))
运行程序,输出如下:
ARI=0.99
效果如下图所示:
图 9 检测异常数据结果
4) K均值
基于聚类的离群点识别方法称为K均值方法,K 均值的主要思想是一个对象是基于聚类的离群点,如果该对象不属于任何簇,那么该对象属于离群点。离群点对初始聚类有一定的影响。如果通过聚类检测离群点,则由于离群点影响聚类,存在一个问题:结构是否有效。这也是 K均值算法的缺点,对离群点敏感。为了处理该问题,可以使用对象聚类、删除离群点、对象再次聚类(不能保证产生最优结果)等方法。
K 均值检测离群点存在的优缺点主要表现在:
- 基于线性和接近线性复杂度(K 均值)的聚类技术来发现离群点可能是高度有效的;
- 簇的定义通常是离群点的补充,因此可能同时发现簇和离群点;
- 产生的离群点集和它们的值可能非常依赖所用的簇的个数和数据中离群点的存在性;
- 聚类算法产生的簇的质量对该算法产生的离群点的质量影响非常大。
【实例】K 均值聚类检测离群点。
# 导入第三方包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.preprocessing import scale
# 随机生成两组二元正态分布随机数
np.random.seed(1234)
mean1 = [0.5, 0.5]
cov1 = [[0.3, 0], [0, 0.1]]
x1, y1 = np.random.multivariate_normal(mean1, cov1, 5000).T
mean2 = [0, 8]
cov2 = [[0.8, 0], [0, 2]]
x2, y2 = np.random.multivariate_normal(mean2, cov2, 5000).T
# 绘制两组数据的散点图
plt.rcParams['axes.unicode_minus'] = False
plt.scatter(x1, y1)
plt.scatter(x2, y2)
# 显示图形
plt.show()
# 将两组数据集汇总到数据框中
X = pd.DataFrame(np.concatenate([np.array([x1, y1]), np.array([x2, y2])], axis=1).T)
X.rename(columns={0: 'x1', 1: 'x2'}, inplace=True)
# 自定义函数的调用
def kmeans_outliers(data, clusters, is_scale=True):
# 指定聚类个数,准备进行数据聚类
kmeans = KMeans(n_clusters=clusters)
# 用于存储聚类相关的结果
cluster_res = []
# 判断是否需要对数据做标准化处理
if is_scale:
std_data = scale(data) # 标准化
kmeans.fit(std_data) # 聚类拟合
# 返回簇标签
labels = kmeans.labels_
# 返回簇中心
centers = kmeans.cluster_centers_
for label in set(labels):
# 计算簇内样本点与簇中心的距离
diff = std_data[np.array(labels) == label, ] - np.array(centers[label])
dist = np.sum(np.square(diff), axis=1)
# 计算判断异常的阈值
UL = dist.mean() + 3 * dist.std()
# 识别异常值,1表示异常,0表示正常
OutLine = np.where(dist > UL, 1, 0)
raw_data = data.loc[np.array(labels) == label, ]
new_data = pd.DataFrame({'Label': label, 'Dist': dist, 'OutLier': OutLine})
# 重新修正两个数据框的行编号
raw_data.index = new_data.index = range(raw_data.shape[0])
# 数据的列合并
cluster_res.append(pd.concat([raw_data, new_data], axis=1))
else:
kmeans.fit(data) # 聚类拟合
# 返回簇标签
labels = kmeans.labels_
# 返回簇中心
centers = kmeans.cluster_centers_
for label in set(labels):
# 计算簇内样本点与簇中心的距离
diff = np.array(data.loc[np.array(labels) == label, ]) - np.array(centers[label])
dist = np.sum(np.square(diff), axis=1)
UL = dist.mean() + 3 * dist.std()
OutLine = np.where(dist > UL, 1, 0)
raw_data = data.loc[np.array(labels) == label, ]
new_data = pd.DataFrame({'Label': label, 'Dist': dist, 'OutLier': OutLine})
raw_data.index = new_data.index = range(raw_data.shape[0])
cluster_res.append(pd.concat([raw_data, new_data], axis=1))
# 返回数据的行合并结果
return pd.concat(cluster_res)
# 调用函数,返回异常检测的结果
res = kmeans_outliers(X, 2, False)
# 绘图
sns.lmplot(x="x1", y="x2", hue='OutLier', data=res,
fit_reg=False, legend=False)
plt.legend(loc='best')
plt.show()
运行程序,效果如下图所示: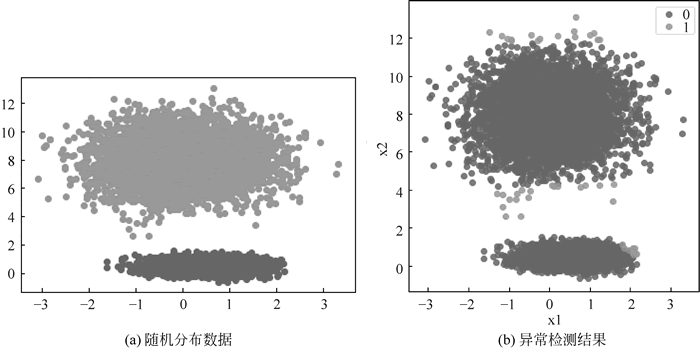
图 10 K均值异常检测处理
5) 孤立森林
孤立森林是一种无监督学习算法,属于组合决策树家族。前面介绍的算法都在试图寻找数据的常规区域,然后将任何在此定义区域之外的点都视为离群点或异常值。孤立森林与其他算法不同,这种算法的工作方式较特别,它明确地隔离异常值,不需要通过为每个数据点分配一个分数来分析和构造正常的点和区域。
孤立森林的异常值只是少数,并且它们具有与正常实例非常不同的属性值。该算法适用于高维数据集,并且被证明是一种非常有效的异常检测方法。
【实例】利用孤立森林检测数据异常值。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
rng = np.random.RandomState(42)
# 创建训练数据
X = 0.3 * rng.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
# 生成一些常规的新观察结果
X = 0.3 * rng.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
# 生成一些异常的新观察结果
X_outliers = rng.uniform(low=-4, high=4, size=(20, 2))
# 拟合模型
clf = IsolationForest(max_samples=100, random_state=rng)
clf.fit(X_train)
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)
# 绘制决策边界
xx, yy = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.title("孤立森林")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white',
s=20, edgecolor='k', marker='p')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='green',
s=20, edgecolor='k', marker='s')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='red',
s=20, edgecolor='k', marker='o')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([b1, b2, c],
["训练观察",
"新的常规观察", "新的异常观察"],
loc="upper left")
plt.show()
运行程序,效果如下图所示: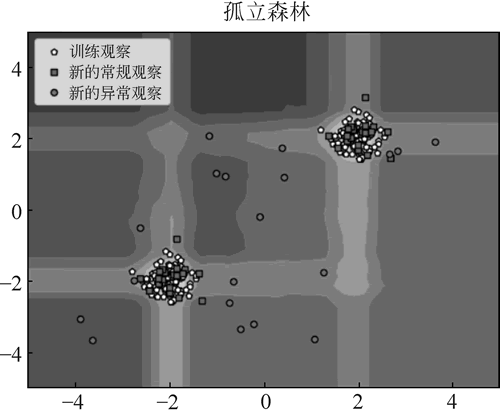
图 11 孤立森林检测异常点效果
其中,图 11 中的圆点即为异常点,五边形是训练集,正方形是测试数据。
2、异常值如何处理
异常值被检测出来后还需要进一步确认,确认是真正的异常值后才会对其进行处理。常用处理方式如下:- 删除异常值——drop方法;
- 替换异常值——replace方法。
1) drop方法删除异常值
pandas 提供 drop 方法,可按指定行索引或列索引来删除异常值。函数的语法格式为:DataFrame.drop(labels=None,axis=0,index=None,columns=None,level=None,inplace=False,errors='raise')其中:
- labels 参数:表示要删除的行索引或列索引,可以删除一个或多个。
- axis 参数:指定删除行或删除列。
- index 参数:指定要删除的行。
- columns:指定要删除的列。
2) replace方法替换异常值
该函数的语法格式为:DataFrame.replace(to_replace=None,Value=None,inplace=False,limit=None,regex=False,method='pad')其中:
- to_place:表示被替换的值;
- value:表示被替换后的值,默认为 None;
- inplace:表示是否修改原数据;
- method:表示替换方式,取 'pad/ffill',表示向前填充;取 'bfill',表示向后填充。
【实例】异常值处理。
分析:假设有 dataset.xlsx 文件,记录了班级同学的成绩,部分数据如下图所示。
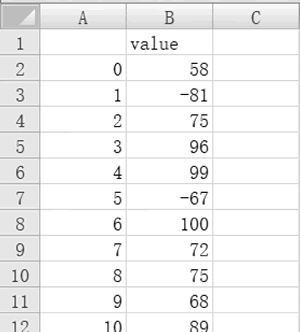
图 12 部分同学的成绩
很明显可以看到行索引为 1 和行索引为 5 的分数值明显超出正常范围,所以希望通过 3σ 准则用代码把这两个“例外”找出来。
import numpy as np
import pandas as pd
def three_sigma(ser):
'''
ser参数:被检测的数据,接收DataFrame的一列数据
返回:异常值及其对应的行索引
'''
# 计算平均值
mean_data = ser.mean()
# 计算标准差
std_data = ser.std()
# 小于μ-3σ或大于μ+3σ的数据均为异常值
rule = (mean_data - 3 * std_data > ser) | (mean_data + 3 * std_data < ser)
# np.arange方法生成一个从0开始到ser长度-1结束的连续索引,再根据rule列表中的True值,
# 直接保留所有为True的索引,也就是异常值的行索引
index = np.arange(ser.shape[0])[rule]
# 获取异常值
outliers = ser.iloc[index]
return outliers
# 读取data.xlsx文件
excel_data = pd.read_excel('dataset.xlsx')
# 对value列进行异常值检测,只要传入一个数据列
three_sigma(excel_data['value'])
运行程序,输出如下:
1 -81
5 -67
Name:value,dtype:int64
3) 使用箱形图检测异常值
import pandas as pd
excel_data=pd.read_excel('dataset.xlsx')
#根据data.xlsx文件中value列的数据,画一个箱形图
excel_data.boxplot(column='value')
运行程序,效果如下图所示:
图 13 箱形图
从图 13 可以看到两个圆圈表示的两个异常值。
下面的代码实现:
- 定义一个从箱形图中获取异常值的函数 box_outliners;
- 返回文件中数据的异常值及其对应的索引。
import pandas as pd
import numpy as np
def box_outliers(ser):
# 对待检测的数据集进行排序
new_ser = ser.sort_values()
# 判断数据的总数量是奇数还是偶数
if new_ser.count() % 2 == 0:
# 计算Q3,Q1,IQR
Q3 = new_ser[int(len(new_ser) / 2):].median()
Q1 = new_ser[:int(len(new_ser) / 2)].median()
elif new_ser.count() % 2 != 0:
Q3 = new_ser[int(len(new_ser) / 2 - 1):].median()
Q1 = new_ser[:int(len(new_ser) / 2 - 1)].median()
IQR = round(Q3 - Q1, 1)
rule = (round(Q3 + 1.5 * IQR, 1) < ser) | (round(Q1 - 1.5 * IQR, 1) > ser)
index = np.arange(ser.shape[0])[rule]
# 获取异常值及其索引
outliers = ser.iloc[index]
return outliers
# 读取Excel文件
excel_data = pd.read_excel('dataset.xlsx')
# 检测异常值
box_outliers(excel_data['value'])
运行程序,输出如下:
1 -81
5 -67
Name:value,dtype:int64
4) 删除异常值
删除异常值后,可以再次调用自定义的异常值检测函数,以确保数据中的异常值全部被删除。代码演示如下:
#根据上面自定义函数得到的异常值行索引,来删除异常值 clean_data=excel_data.drop([1, 5]) #再次检测数据中是否还有异常值 three_sigma(clean_data['value'])运行程序,输出如下:
Series([], Name:value, dtype:int64)
则说明异常值已经全部删除成功。5) 替换异常值
假设要对前面的成绩单中的异常值进行处理,负值处理为 0 分,超过 100 分的统一按 100 分计算。
replace_data=excel_data.replace({-100:0, 200:100})
#根据行索引获取替换后的值
print(replace_data.loc[1])
print(replace_data.loc[5])
运行程序,输出如下:
value -81
Name:1,dtype:int64
value -67
Name:5,dtype:int64
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: