哈夫曼编码详解(Java实现)
哈夫曼编码通常应用在数据通信中,在数据传送时,需要将字符转换为二进制的字符串。
例如,假设传送的电文是 ABDAACDA,电文中有 A、B、C 和 D 共 4 种字符,若规定 A、B、C 和 D 的编码分别为 00、01、10 和 11,则上面的电文代码为 0001110000101100,总共 16 个二进制数。
在传送电文时,希望电文的代码尽可能短。如果按照每个字符进行长度不等的编码,将出现频率高的字符采用尽可能短的编码,电文的代码长度就会减小。可以利用哈夫曼树对电文进行编码,最后得到的编码就是长度最短的编码。
接下来是具体的构造方法。假设需要编码的字符集合为 {c1,c2,…,cn},相应地,字符在电文中的出现次数为 {w1,w2,…,wn},以字符 c1,c2,…,cn 作为叶子结点,以 w1,w2,…,wn 为对应叶子结点的权值构造一棵二叉树,规定哈夫曼树的左孩子分支为 0,右孩子分支为 1,从根结点到每个叶子结点经过的分支组成的 0 和 1 序列就是结点对应的编码。
按照以上构造方法,字符集合为 {A,B,C,D},各个字符相应出现的次数为 {4,1,1,2},这些字符作为叶子结点构成的哈夫曼树如下图所示。
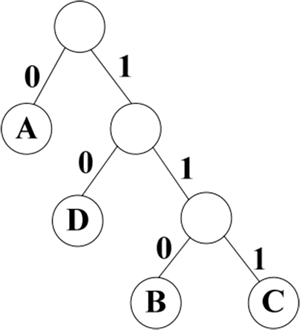
图 1 哈夫曼编码
字符 A 的编码为 0,字符 B 的编码为 110,字符 C 的编码为 111,字符 D 的编码为 10。
因此,可以得到电文 ABDAACDA 的哈夫曼编码为 01101000111100,共 13 个二进制字符。这样就保证了电文的编码达到最短。
在设计不等长编码时,必须使任何一个字符的编码都不是另一个字符的编码的前缀。例如,字符 A 的编码为 10,字符 B 的编码为 100,则字符 A 的编码就称为字符 B 的编码的前缀。如果一个代码为 10010,在进行译码时,无法确定是将前两位译为 A,还是将前三位译为 B。
但是在利用哈夫曼树进行编码时,每个编码是叶子结点的编码,一个字符不会出现在另一个字符的前面,也就不会出现一个字符的编码是另一个字符的编码的前缀编码。
【实例】假设一个字符序列为 {A,B,C,D},对应的权重为 {1,3,6,9}。设计一个哈夫曼树,并输出相应的哈夫曼编码。
在哈夫曼算法中,为了设计方便,利用一个二维数组来实现。需要保存字符的权重、双亲结点的位置、左孩子结点的位置和右孩子结点的位置。因此,需要设计 n 行 4 列。哈夫曼树的类型定义如下:
依次选择两个权值最小的结点,分别作为左子树结点和右子树结点,修改它们的双亲结点域,使它们指向同一个双亲结点,同时修改双亲结点的权值,使其等于两个左、右子树结点权值的和,并修改左、右孩子结点域,使其分别指向左、右孩子结点。
重复执行这种操作 n-1 次,即可求出 n-1 个非叶子结点的权值。这样就得到了一棵哈夫曼树。
通过已经构造的哈夫曼树,得到每个叶子结点的哈夫曼编码。从叶子结点 c 开始,通过结点 c 的双亲结点域找到结点的双亲,然后通过双亲结点的左孩子域和右孩子域判断该结点 c 是其双亲结点的左孩子还是右孩子,若是左孩子,则编码为 0,否则编码为 1。按照这种方法,直到找到根结点,即可求出叶子结点的编码。
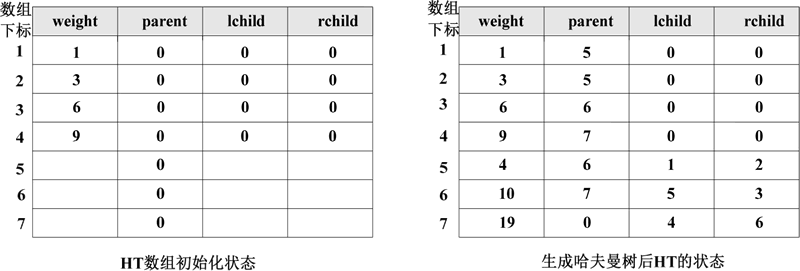
图 2 数组 HT 在初始化和生成哈夫曼树后的状态变化
生成的哈夫曼树如下图所示。从图中可以看出,权值为 1、3、6 和 9 的哈夫曼编码分别是 100、101、11 和 0。
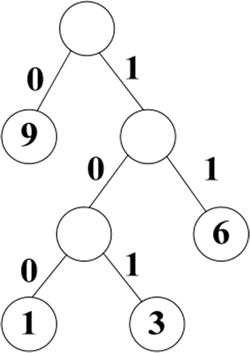
图 3 哈夫曼树
例如,假设传送的电文是 ABDAACDA,电文中有 A、B、C 和 D 共 4 种字符,若规定 A、B、C 和 D 的编码分别为 00、01、10 和 11,则上面的电文代码为 0001110000101100,总共 16 个二进制数。
在传送电文时,希望电文的代码尽可能短。如果按照每个字符进行长度不等的编码,将出现频率高的字符采用尽可能短的编码,电文的代码长度就会减小。可以利用哈夫曼树对电文进行编码,最后得到的编码就是长度最短的编码。
接下来是具体的构造方法。假设需要编码的字符集合为 {c1,c2,…,cn},相应地,字符在电文中的出现次数为 {w1,w2,…,wn},以字符 c1,c2,…,cn 作为叶子结点,以 w1,w2,…,wn 为对应叶子结点的权值构造一棵二叉树,规定哈夫曼树的左孩子分支为 0,右孩子分支为 1,从根结点到每个叶子结点经过的分支组成的 0 和 1 序列就是结点对应的编码。
按照以上构造方法,字符集合为 {A,B,C,D},各个字符相应出现的次数为 {4,1,1,2},这些字符作为叶子结点构成的哈夫曼树如下图所示。

图 1 哈夫曼编码
字符 A 的编码为 0,字符 B 的编码为 110,字符 C 的编码为 111,字符 D 的编码为 10。
因此,可以得到电文 ABDAACDA 的哈夫曼编码为 01101000111100,共 13 个二进制字符。这样就保证了电文的编码达到最短。
在设计不等长编码时,必须使任何一个字符的编码都不是另一个字符的编码的前缀。例如,字符 A 的编码为 10,字符 B 的编码为 100,则字符 A 的编码就称为字符 B 的编码的前缀。如果一个代码为 10010,在进行译码时,无法确定是将前两位译为 A,还是将前三位译为 B。
但是在利用哈夫曼树进行编码时,每个编码是叶子结点的编码,一个字符不会出现在另一个字符的前面,也就不会出现一个字符的编码是另一个字符的编码的前缀编码。
哈夫曼编码算法的实现
下面利用哈夫曼编码的设计思想,通过一个实例实现哈夫曼编码的算法。【实例】假设一个字符序列为 {A,B,C,D},对应的权重为 {1,3,6,9}。设计一个哈夫曼树,并输出相应的哈夫曼编码。
在哈夫曼算法中,为了设计方便,利用一个二维数组来实现。需要保存字符的权重、双亲结点的位置、左孩子结点的位置和右孩子结点的位置。因此,需要设计 n 行 4 列。哈夫曼树的类型定义如下:
class HTNode { // 哈夫曼树结点类型定义
int weight;
int parent, lchild, rchild;
HTNode() {
this.weight = weight;
this.parent = parent;
this.lchild = lchild;
this.rchild = rchild;
}
}
定义一个类型为 HuffmanCode 的变量 HT,用来存放每个叶子结点的哈夫曼编码。初始时,将每个叶子结点的双亲结点域、左孩子域和右孩子域初始化为 0。若有 n 个叶子结点,则非叶子结点有 n-1 个,所以总共结点数目是 2n-1 个。同时也要将剩下的 n-1 个双亲结点域初始化为 0,这主要是为了方便查找权值最小的结点。依次选择两个权值最小的结点,分别作为左子树结点和右子树结点,修改它们的双亲结点域,使它们指向同一个双亲结点,同时修改双亲结点的权值,使其等于两个左、右子树结点权值的和,并修改左、右孩子结点域,使其分别指向左、右孩子结点。
重复执行这种操作 n-1 次,即可求出 n-1 个非叶子结点的权值。这样就得到了一棵哈夫曼树。
通过已经构造的哈夫曼树,得到每个叶子结点的哈夫曼编码。从叶子结点 c 开始,通过结点 c 的双亲结点域找到结点的双亲,然后通过双亲结点的左孩子域和右孩子域判断该结点 c 是其双亲结点的左孩子还是右孩子,若是左孩子,则编码为 0,否则编码为 1。按照这种方法,直到找到根结点,即可求出叶子结点的编码。
1) 构造哈夫曼树
public void CreateHuffmanTree(HTNode HT[], int w[], int n) // 构造哈夫曼树 HT,哈夫曼树的编码存放在 HC 中,w 为 n 个字符的权值
{
if (n <= 1)
return;
int m = 2 * n - 1;
for (int i = 1; i <= n; i++) // 初始化 n 个叶子结点
{
HT[i] = new HTNode();
HT[i].weight = w[i - 1];
HT[i].parent = 0;
HT[i].lchild = HT[i].rchild = 0;
}
for (int i = n + 1; i <= m; i++) // 将 n - 1 个非叶子结点的双亲结点初始化为 0
{
HT[i] = new HTNode();
HT[i].parent = 0;
}
for (int i = n + 1; i <= m; i++) // 构造哈夫曼树
{
List<Integer> s = Select(HT, i - 1); // 查找树中权值最小的两个结点
int s1 = s.get(0), s2 = s.get(1);
HT[s1].parent = i;
HT[s2].parent = i;
HT[i].lchild = s1;
HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight;
}
}
2) 利用哈夫曼树进行哈夫曼编码
public void HuffmanCoding(HTNode HT[], String HC[], int w[], int n)
// 从叶子结点到根结点求每个字符的哈夫曼编码,哈夫曼树的编码存放在 HC 中,w 为 n 个字符的权值
{
for(int i=1; i<=n; i++)
{
char cd[]=new char[n+1];
int start=n-1;
for(int c=i, f=HT[i].parent; f!=0; c=f, f=HT[f].parent) // 从叶子结点到根结点求编码
{
if (HT[f].lchild == c)
cd[--start] = '0';
else
cd[--start] = '1';
}
HC[i]=new String();
String str=new String(cd);
HC[i]=str; // 将当前求出结点的哈夫曼编码复制到 HC
}
}
3) 查找权值最小和次小的两个结点
这部分主要是在结点的权值中选择权值最小和次小的结点作为二叉树的叶子结点。其程序代码实现如下:
public List Select(HTNode t[], int n)
// 在 n 个结点中选择权值最小和次小的结点序号,其中 s1 最小,s2 次小
{
List result = new ArrayList();
int s1 = Min(t, n);
int s2 = Min(t, n);
if (t[s1].weight > t[s2].weight) // 若序号 s1 的权值大于序号 s2 的权值,则将两者交换,使 s1 最小,s2 次小
{
int x = s1;
s1 = s2;
s2 = x;
}
result.add(s1);
result.add(s2);
return result;
}
public int Min(HTNode t[], int n)
// 返回树中 n 个结点中权值最小的结点序号
{
int f = Integer.MAX_VALUE; // f 为一个无限大的值
int flag = 0;
for (int i = 1; i < n + 1; i++) {
if (t[i].weight < f && t[i].parent == 0) {
f = t[i].weight;
flag = i;
}
}
t[flag].parent = 1; // 给选中的结点的双亲结点赋值 1,避免再次查找该结点
return flag;
}
4) 译码
根据给定的哈夫曼编码,如 100101011,利用哈夫曼树进行译码,得到对应的字符序列。
public void GetStr(HTNode HT[], int m, char w[], char str[]) {
int i = 0, n = 2 * m - 1;
int length = str.length;
for (i = 0; i < length; i++) {
if (str[i] == '1')
n = HT[n].rchild;
else if (str[i] == '0')
n = HT[n].lchild;
else
return;
}
for (int j = 1; j <= m; j++) {
if (j n ==) {
n = 2 * m - 1;
System.out.print(w[j-1] + " ");
break;
}
}
}
5) 测试代码部分
public static void main(String args[]) {
System.out.println("请输入叶子结点的个数:");
Scanner sc = new Scanner(System.in);
int n = Integer.parseInt(sc.nextLine());
int m = 2 * n - 1;
HTNode HT[] = new HTNode[m + 1];
String HC[] = new String[n + 1];
int w[] = new int[n]; // 为 n 个结点的权值分配内存空间
for (int i = 0; i < n; i++) {
System.out.print(String.format("请输入第%d个结点的权值:", i + 1));
w[i] = Integer.parseInt(sc.nextLine());
}
HuffmanTree HTree = new HuffmanTree();
HTree.CreateHuffmanTree(HT, w, n);
for (int i = 1; i <= n; i++) {
System.out.println("哈夫曼编码:" + HC[i]);
}
char wname[] = {'A', 'B', 'C', 'D', 'E', 'F'};
HTree.GetStr(HT, n, wname, "100101011".toCharArray());
}
在算法的实现过程中,其中数组 HT 在初始化状态和生成哈夫曼树后的状态如下图所示。
图 2 数组 HT 在初始化和生成哈夫曼树后的状态变化
生成的哈夫曼树如下图所示。从图中可以看出,权值为 1、3、6 和 9 的哈夫曼编码分别是 100、101、11 和 0。

图 3 哈夫曼树
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: