Matplotlib hist()绘制直方图(附带实例)
直方图又称质量分布图,用一系列高度不等的纵向条纹或线段表示数据的分布情况。一般横轴表示数据类型,纵轴表示数据分布情况。
直方图是数值数据分布的精确图形表示,是连续变量(定量变量)的概率分布估计。
绘制直方图主要使用 hist() 函数,语法格式如下:
下面绘制简单直方图,程序代码如下:
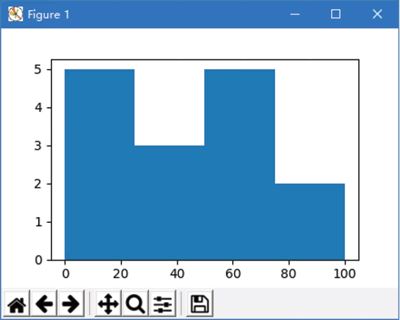
图 1 简单直方图
再例如,通过直方图分析学生数学成绩分布情况,程序代码如下:

图 2 数学成绩分布直方图
在上述示例中,通过直方图可以清晰地看到高一数学成绩分布情况:基本呈现正态分布,两边低中间高,高分段学生缺失,说明试卷有难度。通过直方图还可以分析以下内容:
直方图是数值数据分布的精确图形表示,是连续变量(定量变量)的概率分布估计。
绘制直方图主要使用 hist() 函数,语法格式如下:
matplotlib.pyplot.hist(x,bins=None,range=None,density=None,bottom=None,histtype='bar',align='mid',log=False, color=None, label=None, stacked=False, normed=None)参数说明:
- x:数据集,最终的直方图将对数据集进行统计;
- bins:统计数据的区间分布;
- range:元组类型,显示区间;
- density:布尔值,表示是否显示频率统计结果,默认值为 False,为 True 则显示频率统计结果。需要注意,频率统计结果=区间数目/(总数×区间宽度);
- histtype:可选参数,设置值为 bar、barstacked、step 或 stepfilled,默认值为 bar,推荐使用默认值;
- align:可选参数,值为 left、mid 或 right,默认值为 mid,控制直方图的水平分布,设置为 left 或者 right 时会有部分空白区域,推荐使用默认值;
- log:布尔值,默认值为 False,指明 y 轴是否使用指数刻度;
- stacked:布尔值,默认值为 False,指明是否为堆积状图。
下面绘制简单直方图,程序代码如下:
import matplotlib.pyplot as plt x=[22,87,5,43,56,73,55,54,11,20,51,5,79,31,27] plt.hist(x, bins = [0,25,50,75,100]) plt.show()运行程序,结果如图 1 所示:

图 1 简单直方图
再例如,通过直方图分析学生数学成绩分布情况,程序代码如下:
# 导入相关模块
import pandas as pd
import matplotlib.pyplot as plt
# 读取Excel文件
df = pd.read_excel(io='../datas/grade.xlsx',sheet_name="数学")
plt.rcParams['font.sans-serif']=['SimHei'] # 解决中文乱码问题
x=df['得分'] # x轴数据
plt.xlabel('分数') # x轴标题
plt.ylabel('学生数量') # y轴标题
plt.title('高一数学成绩分布直方图') # 图表标题
# 绘制直方图
plt.hist(x, bins = [0,25,50,75,100,125,150],facecolor="blue", edgecolor="black", alpha=0.7)
plt.show() # 显示图表
运行程序,结果如下图所示:
图 2 数学成绩分布直方图
在上述示例中,通过直方图可以清晰地看到高一数学成绩分布情况:基本呈现正态分布,两边低中间高,高分段学生缺失,说明试卷有难度。通过直方图还可以分析以下内容:
- 对学生进行比较。呈正态分布的结果便于选拔优秀生,甄别落后生;
- 确定人数和分数线。成绩符合正态分布可以帮助确定等级评定人数,估计某分数段内的人数,确定录取分数线、各学科的优秀生占比等;
- 分析测验试题难度。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: