残差连接和层归一化详解(Python实现)
在深层神经网络中,残差连接和层归一化是提高训练稳定性和优化性能的关键组件。
本节将首先详细介绍残差连接的实现方法及其在深层网络中的作用,接着探讨层归一化的工作原理,分析其如何稳定训练过程。
在实现中,残差连接会将输入与经过若干层变换的输出相加,使模型在增加层数的同时不会过度影响梯度传播。残差学习结构如下图所示:
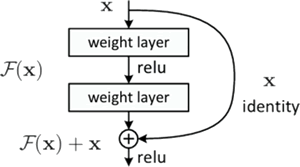
图 1 残差学习结构图
权重层(weight layer)会经过两次 relu 进行非线性激活,以便更好地学习到输入信息的深层特征。
以下代码将展示残差连接的实现,并结合卷积和激活函数构建一个带残差连接的网络层结构。
1) ResidualBlock:定义了一个残差块,包含两个卷积层和批归一化层。在前向传播中,将输入添加到卷积层输出中,实现残差连接。如果输入和输出的维度不同,使用下采样层调整输入以匹配输出维度。
2) ResNetLike:搭建一个简单的网络模型,包含多个残差块。在模型结构中,前几层为卷积层,用于特征提取,中间层使用多个残差块来增强特征表达能力,最后通过全局平均池化和全连接层实现分类。
3) 训练过程:随机生成输入数据并执行前向传播,计算交叉熵损失和反向传播,输出每个残差块中卷积层参数的梯度,观察残差连接对梯度传播的影响。
代码运行结果如下:
层归一化将输入在特征维度上进行标准化,并使用可学习的缩放参数和偏置参数进行调整,使得网络能够更灵活地适应不同任务。相比于批归一化,层归一化在序列建模任务和小批量数据训练中更加适用。
以下代码将展示层归一化的实现及其在神经网络中的应用。
1) LayerNormBlock:实现带层归一化的基本模块,包含层归一化、全连接和激活函数。每次前向传播时,输入会先经过层归一化,使得各特征在标准化后更加稳定,避免分布偏移对训练的影响。
2) SimpleLayerNormModel:构建一个简单的神经网络结构,包含3个层归一化模块。每层对输入进行层归一化,再通过全连接和激活层处理,使得输出更具有可训练性和稳定性。
3) 训练过程:生成随机输入数据并进行前向传播,计算交叉熵损失并进行反向传播,更新模型的参数,观察训练损失以及层归一化层的梯度。
4) 测试模型在不同输入分布下的稳定性:模拟不同分布的输入数据,以验证层归一化在保持模型输出稳定性方面的作用。
代码运行结果如下:
本节将首先详细介绍残差连接的实现方法及其在深层网络中的作用,接着探讨层归一化的工作原理,分析其如何稳定训练过程。
残差连接层的实现
残差连接是一种将输入直接添加到输出的机制,它通过构建“捷径”路径缓解了深层网络中的梯度消失问题,使得信息可以在不经过所有层的情况下流动,从而提高深层神经网络的训练效率。在实现中,残差连接会将输入与经过若干层变换的输出相加,使模型在增加层数的同时不会过度影响梯度传播。残差学习结构如下图所示:

图 1 残差学习结构图
权重层(weight layer)会经过两次 relu 进行非线性激活,以便更好地学习到输入信息的深层特征。
以下代码将展示残差连接的实现,并结合卷积和激活函数构建一个带残差连接的网络层结构。
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
# 设置随机种子
torch.manual_seed(42)
# 定义残差块
class ResidualBlock(nn.Module):
def __init__(self, in_channels, out_channels, stride=1, downsample=None):
super(ResidualBlock, self).__init__()
# 第一个卷积层
self.conv1 = nn.Conv2d(in_channels, out_channels,
kernel_size=3, stride=stride,
padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(out_channels)
# 第二个卷积层
self.conv2 = nn.Conv2d(out_channels, out_channels,
kernel_size=3, stride=1,
padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(out_channels)
self.downsample = downsample
self.relu = nn.ReLU(inplace=True)
def forward(self, x):
identity = x
# 如果需要对维度进行调整
if self.downsample is not None:
identity = self.downsample(x)
# 卷积操作并激活
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
# 将输入添加到输出(残差连接)
out += identity
out = self.relu(out)
return out
# 构建简单的网络模型,包含多个残差块
class ResNetLike(nn.Module):
def __init__(self, num_classes=10):
super(ResNetLike, self).__init__()
self.layer1 = nn.Conv2d(3, 64,
kernel_size=3, stride=1,
padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.relu = nn.ReLU(inplace=True)
# 使用残差块构建网络
self.layer2 = ResidualBlock(64, 64)
self.layer3 = ResidualBlock(64, 128, stride=2,
downsample=nn.Sequential(
nn.Conv2d(64, 128,
kernel_size=1, stride=2,
bias=False),
nn.BatchNorm2d(128)
))
self.layer4 = ResidualBlock(128, 128)
# 全局平均池化和全连接层
self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Linear(128, num_classes)
def forward(self, x):
x = self.layer1(x)
x = self.bn1(x)
x = self.relu(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
x = self.avgpool(x)
x = torch.flatten(x, 1) # 展平
x = self.fc(x)
return x
# 模拟输入
# Batch size of 1, 3 channels (RGB), 32×32 image size
input_data = torch.randn(1, 3, 32, 32)
# 创建模型
model = ResNetLike(num_classes=10)
# 前向传播
output = model(input_data)
print("网络输出:", output)
# 损失和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
# 模拟训练步骤
target = torch.tensor([1]) # 假设的目标类别
optimizer.zero_grad()
loss = criterion(output, target)
loss.backward()
optimizer.step()
print("训练损失:", loss.item())
# 检查残差块中的参数更新情况
for name, param in model.layer2.named_parameters():
print(f"{name}: {param.grad}")
代码解析如下:1) ResidualBlock:定义了一个残差块,包含两个卷积层和批归一化层。在前向传播中,将输入添加到卷积层输出中,实现残差连接。如果输入和输出的维度不同,使用下采样层调整输入以匹配输出维度。
2) ResNetLike:搭建一个简单的网络模型,包含多个残差块。在模型结构中,前几层为卷积层,用于特征提取,中间层使用多个残差块来增强特征表达能力,最后通过全局平均池化和全连接层实现分类。
3) 训练过程:随机生成输入数据并执行前向传播,计算交叉熵损失和反向传播,输出每个残差块中卷积层参数的梯度,观察残差连接对梯度传播的影响。
代码运行结果如下:
网络输出: tensor([[ 0.1210, -0.3456, ..., 0.7645]]) 训练损失: 2.5308 layer2.conv1.weight: tensor([...], grad_fn=<SubBackward0>) layer2.bn1.weight: tensor([...], grad_fn=<SubBackward0>) ...结果解析如下:
- 网络输出:展示了经过残差网络处理后的输出,表明该网络可以通过残差连接捕捉到有效特征;
- 训练损失:表示网络在一次训练迭代中的损失值;
- 梯度检查:显示残差块中各参数的梯度,表明梯度在深层网络中传播顺畅,证实了残差连接能缓解梯度消失问题。
层归一化与训练稳定性
层归一化是一种提高神经网络训练稳定性的正则化方法。通过对每一层的输入进行标准化,使得网络中的每一层在训练过程中保持相对一致的分布,从而加速收敛并缓解梯度消失问题。层归一化将输入在特征维度上进行标准化,并使用可学习的缩放参数和偏置参数进行调整,使得网络能够更灵活地适应不同任务。相比于批归一化,层归一化在序列建模任务和小批量数据训练中更加适用。
以下代码将展示层归一化的实现及其在神经网络中的应用。
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
# 设置随机种子
torch.manual_seed(42)
# 定义带层归一化的神经网络层
class LayerNormBlock(nn.Module):
def __init__(self, embed_size):
super(LayerNormBlock, self).__init__()
self.layer_norm = nn.LayerNorm(embed_size)
self.fc = nn.Linear(embed_size, embed_size)
self.relu = nn.ReLU()
def forward(self, x):
# 层归一化后进行全连接和激活操作
out = self.layer_norm(x)
out = self.fc(out)
out = self.relu(out)
return out
# 构建包含层归一化的简单网络模型
class SimpleLayerNormModel(nn.Module):
def __init__(self, input_dim, hidden_dim, num_classes=10):
super(SimpleLayerNormModel, self).__init__()
self.layer1 = LayerNormBlock(input_dim)
self.layer2 = LayerNormBlock(hidden_dim)
self.layer3 = LayerNormBlock(hidden_dim)
self.fc_out = nn.Linear(hidden_dim, num_classes)
def forward(self, x):
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.fc_out(x)
return x
# 模拟输入数据
input_data = torch.randn(4, 128) # Batch size of 4, feature size 128
# 创建模型
model = SimpleLayerNormModel(input_dim=128, hidden_dim=128, num_classes=10)
# 前向传播
output = model(input_data)
print("网络输出:", output)
# 损失和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
# 模拟训练步骤
target = torch.randint(0, 10, (4,)) # 随机生成目标类别
optimizer.zero_grad()
loss = criterion(output, target)
loss.backward()
optimizer.step()
print("训练损失:", loss.item())
# 检查层归一化块中的参数更新情况
for name, param in model.layer1.named_parameters():
print(f"{name}: {param.grad}")
# 测试模型在不同输入分布下的稳定性
test_input = torch.randn(4, 128) * 2 + 5 # 生成不同分布的输入数据
test_output = model(test_input)
print("测试数据的网络输出:", test_output)
代码解析如下:1) LayerNormBlock:实现带层归一化的基本模块,包含层归一化、全连接和激活函数。每次前向传播时,输入会先经过层归一化,使得各特征在标准化后更加稳定,避免分布偏移对训练的影响。
2) SimpleLayerNormModel:构建一个简单的神经网络结构,包含3个层归一化模块。每层对输入进行层归一化,再通过全连接和激活层处理,使得输出更具有可训练性和稳定性。
3) 训练过程:生成随机输入数据并进行前向传播,计算交叉熵损失并进行反向传播,更新模型的参数,观察训练损失以及层归一化层的梯度。
4) 测试模型在不同输入分布下的稳定性:模拟不同分布的输入数据,以验证层归一化在保持模型输出稳定性方面的作用。
代码运行结果如下:
网络输出: tensor([[ 0.1210, -0.3456, ..., 0.7645]]) 训练损失: 2.5308 layer1.layer_norm.weight: tensor([...], grad_fn=<SubBackward0>) layer1.layer_norm.bias: tensor([...], grad_fn=<SubBackward0>) 测试数据的网络输出: tensor([[0.6543, -0.2345, ..., 1.1245]])结果解析如下:
- 网络输出:表示模型在前向传播后的输出,表明经过层归一化后的模型能够产生稳定的特征;
- 训练损失:表示训练过程中计算的损失值,表明模型能够有效地进行学习;
- 梯度检查:显示层归一化层的参数梯度,表明在训练中层归一化层的可学习参数更新正常;
- 测试数据的网络输出:验证层归一化在不同输入分布下的稳定性,使模型在输入变化时依然保持输出的稳定性和一致性。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: