Python绘制折线图(附带实例)
折线图(Line Chart)用于显示随时间、顺序或其他连续变量变化的趋势和模式。它通过连接数据点来展示数据的变化,并利用直线段来表示数据的趋势。
折线图的优点是能够清晰地展示变量随时间或顺序的变化趋势,它可以帮助观察者识别趋势、周期性、增长或下降等模式。它常用于分析时间序列数据、比较不同组的趋势、展示实验结果的变化等。
【实例 1】通过绘制的折线图查看 1949-1969 年间航空客运量的变化情况。输入如下代码:
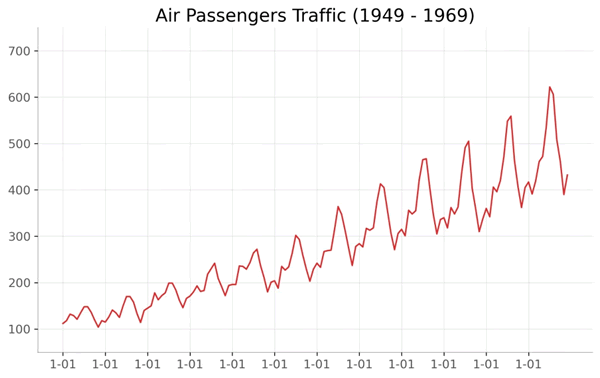
图 1 折线图1
【实例 2】绘制带波峰波谷标记的折线图,并注释所选特殊事件的发生。输入如下代码:
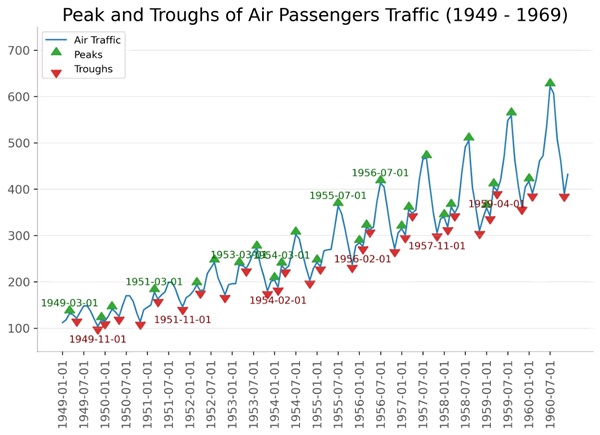
图 2 折线图2
【实例 3】绘制折线图,并将时间序列分解为趋势、季节和残差分量。输入如下代码:
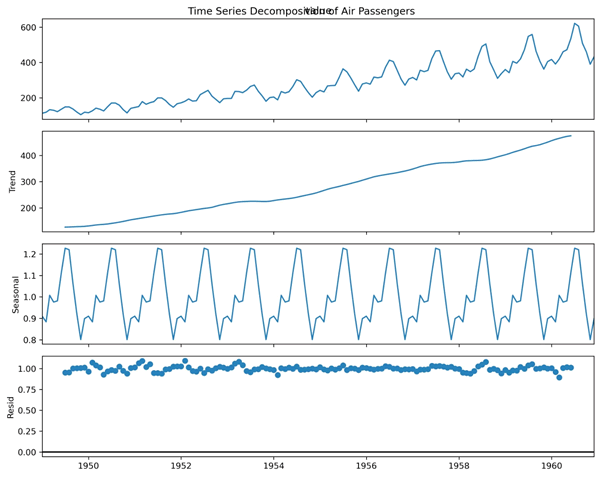
图 3 折线图3
【实例 4 】在同一图表上绘制多条折线图,表征多个时间序列。输入如下代码:
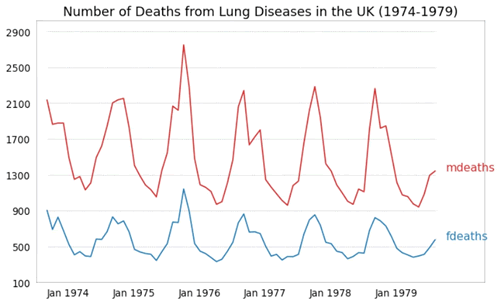
图 4 多条折线图
【实例 5】数据集中每个时间点(日期/时间戳)有多个观测值,请计算 95% 置信区间,并试着构建带有误差带的折线图(时间序列)。输入如下代码:
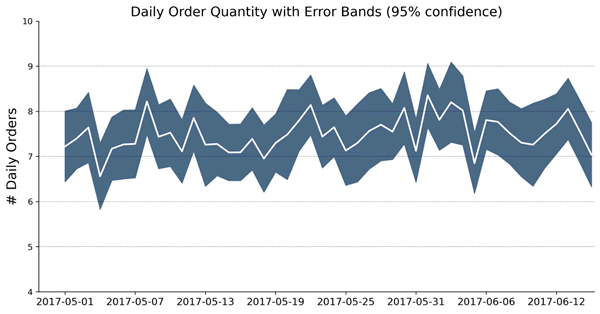
图 5 带误差带的折线图
【实例 6】创建一个包含三个子图的布局,用于可视化随机信号数据的不同视图。输入如下代码:
输出的结果如下图所示:
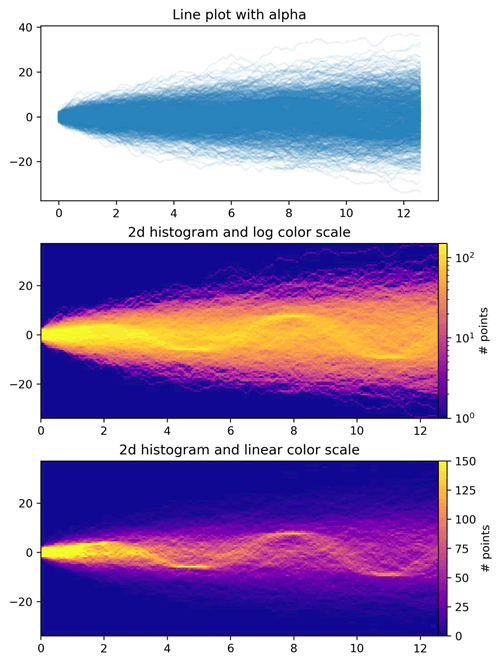
图 6 可视化随机信号
【实例 7】当在同一时间点测量两个不同数量的时间序列时,可以在右侧的辅助 Y 轴上再绘制第 2 个系列,即绘制多 Y 轴图。
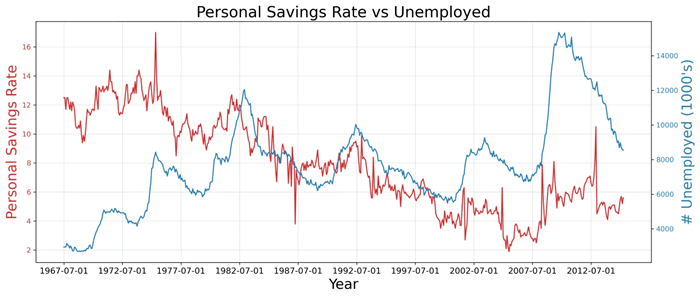
图 7 双Y轴图
折线图的优点是能够清晰地展示变量随时间或顺序的变化趋势,它可以帮助观察者识别趋势、周期性、增长或下降等模式。它常用于分析时间序列数据、比较不同组的趋势、展示实验结果的变化等。
【实例 1】通过绘制的折线图查看 1949-1969 年间航空客运量的变化情况。输入如下代码:
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('D:/DingJB/PyData/AirPassengers.csv') # 导入数据
plt.figure(figsize=(10, 6), dpi=300) # 绘制图表
plt.plot('date', 'value', data=df, color='tab:red') # 绘制折线图
# 图表修饰
plt.ylim(50, 750) # 设置 Y 轴范围
# 设置 X 轴刻度位置和标签
xtick_location = df.index.tolist()[::12]
xtick_labels = [x[-4:] for x in df.date.tolist()[::12]]
plt.xticks(ticks=xtick_location, labels=xtick_labels, rotation=0,
fontsize=12, horizontalalignment='center', alpha=.7)
plt.yticks(fontsize=12, alpha=.7) # 设置 Y 轴刻度标签的字体大小和透明度
plt.title("Air Passengers Traffic (1949-1969)", fontsize=18) # 设置标题
plt.grid(axis='both', alpha=.3) # 添加网格线,设置透明度
# 移除边框
plt.gca().spines["top"].set_alpha(0.0)
plt.gca().spines["bottom"].set_alpha(0.3)
plt.gca().spines["right"].set_alpha(0.0)
plt.gca().spines["left"].set_alpha(0.3)
plt.show()
上述代码首先读取包含空乘客流量数据的 CSV 文件,然后绘制出空乘客流量随时间变化的折线图,并对图表进行修饰,包括设置图表尺寸、添加网格线、设置刻度标签等。输出的结果如下图所示。
图 1 折线图1
【实例 2】绘制带波峰波谷标记的折线图,并注释所选特殊事件的发生。输入如下代码:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
df = pd.read_csv('D:/DingJB/PyData/AirPassengers.csv') # 导入数据
data = df['value'].values # 获取峰值和谷值的位置
# 计算一阶差分
doublediff = np.diff(np.sign(np.diff(data)))
peak_locations = np.where(doublediff == -2)[0] + 1
# 计算负数序列的一阶差分
doublediff2 = np.diff(np.sign(np.diff(-1 * data)))
trough_locations = np.where(doublediff2 == -2)[0] + 1
plt.figure(figsize=(10, 6), dpi=300) # 绘制图表
# 绘制折线图
plt.plot('date', 'value', data=df, color='tab:blue', label='Air Traffic')
# 绘制峰值和谷值的散点图
plt.scatter(df.date[peak_locations], df.value[peak_locations],
marker=mpl.markers.CARETUPBASE, color='tab:green',
s=100, label='Peaks')
plt.scatter(df.date[trough_locations], df.value[trough_locations],
marker=mpl.markers.CARETDOWNBASE, color='tab:red', s=100,
label='Troughs')
# 添加标注
for t, p in zip(trough_locations[1:5], peak_locations[:3]):
plt.text(df.date[p], df.value[p] + 15, df.date[p],
horizontalalignment='center', color='darkgreen')
plt.text(df.date[t], df.value[t] - 35, df.date[t],
horizontalalignment='center', color='darkred')
# 图表修饰
plt.ylim(50, 750)
xtick_location = df.index.tolist()[::6]
xtick_labels = df.date.tolist()[::6]
plt.xticks(ticks=xtick_location, labels=xtick_labels, rotation=90,
fontsize=12, alpha=.7)
plt.yticks(fontsize=12, alpha=.7)
plt.title("Peak and Troughs of Air Passengers Traffic (1949-1969)",
fontsize=18)
plt.yticks(fontsize=12, alpha=.7)
# 变化边框
plt.gca().spines["top"].set_alpha(0.0)
plt.gca().spines["bottom"].set_alpha(0.3)
plt.gca().spines["right"].set_alpha(0.0)
plt.gca().spines["left"].set_alpha(0.3)
# 添加图例、网格和显示图表
plt.legend(loc='upper left')
plt.grid(axis='y', alpha=.3)
plt.show()
上述代码通过读取空乘客流量数据,计算并标注数据中的峰值和谷值位置,然后绘制了空乘客流量随时间变化的折线图,并在图上突出显示了峰值和谷值,以便观察数据的波动情况。输出的结果如下图所示。
图 2 折线图2
【实例 3】绘制折线图,并将时间序列分解为趋势、季节和残差分量。输入如下代码:
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
from dateutil.parser import parse
# 导入数据
df = pd.read_csv('D:/DingJB/PyData/AirPassengers.csv')
dates = pd.DatetimeIndex([parse(d).strftime('%Y-%m-01') for d in df['date']])
df.set_index(dates, inplace=True)
# 分解时间序列
result = seasonal_decompose(df['value'], model='multiplicative')
# 绘图
plt.rcParams.update({'figure.figsize': (10, 8)})
result.plot().suptitle('Time Series Decomposition of Air Passengers')
plt.show()
上述代码利用季节性分解方法对空乘客流量时间序列进行分解,包括趋势、季节性和残差成分,并绘制了相应的图表,以便观察每个成分在时间序列中的变化趋势。输出的结果如下图所示。
图 3 折线图3
【实例 4 】在同一图表上绘制多条折线图,表征多个时间序列。输入如下代码:
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('D:/DingJB/PyData/mortality.csv') # 导入数据
# 定义 Y 轴的上限、下限、间隔和颜色
y_LL = 100 # Y 轴的下限
y_UL = int(df.iloc[:, 1:].max().max() * 1.1) # Y 轴的上限,取数据中最大值的 1.1 倍
y_interval = 400 # Y 轴刻度的间隔
mycolors = ['tab:red', 'tab:blue', 'tab:green', 'tab:orange'] # 折线颜色
fig, ax = plt.subplots(1, 1, figsize=(10, 6), dpi=80) # 创建图表
# 遍历每列数据,绘制折线图并添加标签
columns = df.columns[1:]
for i, column in enumerate(columns):
plt.plot(df.date.values, df[column].values, lw=1.5, color=mycolors[i]) # 绘制折线图
plt.text(df.shape[0] + 1, df[column].values[-1], column, fontsize=14, color=mycolors[i]) # 添加标签
# 绘制刻度线
for y in range(y_LL, y_UL, y_interval):
plt.hlines(y, xmin=0, xmax=71, colors='black', alpha=0.3, linestyles="--", lw=0.5) # 绘制水平线
# 图表修饰
plt.tick_params(axis="both", which="both", bottom=False, top=False,
labelbottom=True, left=False, right=False, labelleft=True) # 设置刻度线参数
# 美化边框
plt.gca().spines["top"].set_alpha(.3)
plt.gca().spines["bottom"].set_alpha(.3)
plt.gca().spines["right"].set_alpha(.3)
plt.gca().spines["left"].set_alpha(.3)
plt.title('Number of Deaths from Lung Diseases in the UK (1974-1979)', fontsize=16) # 添加标题
plt.yticks(range(y_LL, y_UL, y_interval), [str(y) for y in range(y_LL, y_UL, y_interval)]) # 设置 Y 轴刻度及标签
plt.xticks(range(0, df.shape[0], 12), df.date.values[::12], horizontalalignment='left', fontsize=12) # 设置 X 轴刻度及标签
plt.ylim(y_LL, y_UL) # 设置 Y 轴范围
plt.xlim(-2, 80) # 设置 X 轴范围
plt.show()
上述代码读取了一份关于肺部疾病死亡人数的数据,绘制了 1974-1979 年期间的时间序列折线图。每条折线代表不同类型的肺部疾病,如红色表示呼吸道肿瘤、蓝色表示呼吸性肺炎等。图表展示了每种疾病在该时间段内的死亡人数变化情况,并通过标签指示每种疾病的名称。输出的结果如下图所示。
图 4 多条折线图
【实例 5】数据集中每个时间点(日期/时间戳)有多个观测值,请计算 95% 置信区间,并试着构建带有误差带的折线图(时间序列)。输入如下代码:
from scipy.stats import sem # 导入 sem 函数,用于计算标准误差
import pandas as pd
import matplotlib.pyplot as plt
# 导入数据
df_raw = pd.read_csv('D:/DingJB/PyData/orders_45d.csv')
parse_dates = ['purchase_time', 'purchase_date']
# 准备数据:每日订单数量的平均值和标准误差带
df_mean = df_raw.groupby('purchase_date').quantity.mean() # 计算每日订单数量的均值
df_se = df_raw.groupby('purchase_date').quantity.apply(sem).mul(1.96) # 计算每日订单数量的标准误差,并乘以 1.96 得到 95% 置信区间
# 绘图
plt.figure(figsize=(12, 6), dpi=300)
plt.ylabel("# Daily Orders", fontsize=16)
x = [d.date().strftime('%Y-%m-%d') for d in df_mean.index] # 提取每日日期并转换为字符串格式
plt.plot(x, df_mean, color="white", lw=2) # 绘制每日订单数量的折线图
plt.fill_between(x, df_mean - df_se, df_mean + df_se, color="#3F5D7D") # 填充 95% 置信区间
# 图表修饰
# 美化边框
plt.gca().spines["top"].set_alpha(0)
plt.gca().spines["bottom"].set_alpha(1)
plt.gca().spines["right"].set_alpha(0)
plt.gca().spines["left"].set_alpha(1)
plt.xticks(x[:6], [str(d) for d in x[:6]], fontsize=12) # 设置 X 轴刻度及标签
plt.title("Daily Order Quantity with Error Bands (95% confidence)", fontsize=16)
# 设定坐标限制
sx = plt.gca().get_xlim()
plt.xlim(sx[0], sx[1])
plt.ylim(4, 10)
# 绘制水平刻度线
for y in range(5, 10, 1):
plt.hlines(y, xmin=sx[0], xmax=sx[1], colors='black', alpha=0.5, linestyles="--", lw=0.5) # 绘制水平虚线
plt.show()
上述代码从 CSV 文件中读取了订单数据,计算了每日订单数量的平均值和标准误差,并绘制了带有 95% 置信区间的每日订单数量折线图。图表展示了每日订单数量的变化趋势,并突出显示了置信区间,以反映数据的不确定性。输出的结果如下图所示。
图 5 带误差带的折线图
【实例 6】创建一个包含三个子图的布局,用于可视化随机信号数据的不同视图。输入如下代码:
import time
import matplotlib.pyplot as plt
import numpy as np
# 创建一个 3x1 的子图布局
fig, axes = plt.subplots(nrows=3, figsize=(6, 8), layout='constrained')
np.random.seed(19781101) # 固定随机数种子,以便结果可复现
# 生成一些数据,一维随机游走 + 微小部分正弦波
num_series = 1000
num_points = 100
SNR = 0.10 # 信噪比
x = np.linspace(0, 4 * np.pi, num_points)
# 生成无偏高斯随机游走
Y = np.cumsum(np.random.randn(num_series, num_points), axis=1)
# 生成正弦信号
num_signal = round(SNR * num_series)
phi = (np.pi / 8) * np.random.randn(num_signal, 1) # 小的随机偏移
Y[-num_signal:] = (np.sqrt(np.arange(num_points)) * (np.sin(x - phi) + 0.05 * np.random.randn(num_points))) # 小的随机噪声
# 使用 'plot' 绘制系列,并使用小值的 'alpha'
# 因为有太多重叠的系列在该视图中,所以很难观察到正弦行为
tic = time.time()
axes[0].plot(x, Y.T, color="C0", alpha=0.1)
toc = time.time()
axes[0].set_title("Line plot with alpha")
print(f"{toc - tic:.3f} sec. elapsed")
# 将多个时间序列转换为直方图。不仅隐藏的信号更容易看到,而且这是一个更快的过程
toc = time.time()
# 在每个时间序列中的点之间进行线性插值
num_fine = 800
x_fine = np.linspace(x.min(), x.max(), num_fine)
y_fine = np.concatenate([np.interp(x_fine, x, y_row) for y_row in Y])
x_fine = np.broadcast_to(x_fine, (num_series, num_fine)).ravel()
# 使用对数颜色标度在 2D 直方图中绘制 (x, y) 点,可以看出,噪声下存在某种结构
# 调整 vmax 使信号更可见
cmap = plt.get_cmap('plasma')
cmap = cmap.with_extremes(bad=cmap(0))
h, xedges, yedges = np.histogram2d(x_fine, y_fine, bins=[400, 100])
pc = axes[1].pcolormesh(xedges, yedges, h.T, cmap=cmap, norm="log", vmax=1.5e2, rasterized=True)
fig.colorbar(pc, ax=axes[1], label="# points", pad=0)
axes[1].set_title("2D histogram and log color scale")
# 线性颜色标度下的相同数据
pc = axes[2].pcolormesh(xedges, yedges, h.T, cmap=cmap, vmax=1.5e2, rasterized=True)
fig.colorbar(pc, ax=axes[2], label="# points", pad=0)
axes[2].set_title("2D histogram and linear color scale")
toc = time.time()
print(f"{toc - tic:.3f} sec. elapsed")
plt.show()
上述代码创建了一个包含三个子图的图形,展示了不同数据可视化方法的效果:
- 首先,使用透明度(alpha)绘制了具有一定信噪比的大量时间序列数据的折线图;
- 然后,将这些数据转换为二维直方图,并使用对数颜色标度展示了数据的分布情况;
- 最后,展示了相同数据的二维直方图,但使用线性颜色标度展示。
输出的结果如下图所示:

图 6 可视化随机信号
【实例 7】当在同一时间点测量两个不同数量的时间序列时,可以在右侧的辅助 Y 轴上再绘制第 2 个系列,即绘制多 Y 轴图。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv("D:/DingJB/PyData/economics.csv") # 导入数据
x = df['date']
y1 = df['psavert']
y2 = df['unemploy']
# 绘制线条 1(左 Y 轴)
fig, ax1 = plt.subplots(1, 1, figsize=(14, 6), dpi=300)
ax1.plot(x, y1, color='tab:red')
# 绘制线条 2(右 Y 轴)
ax2 = ax1.twinx() # 实例化一个共享相同 X 轴的第 2 个坐标轴
ax2.plot(x, y2, color='tab:blue')
# 图表修饰
# ax1(左 Y 轴)
ax1.set_xlabel('Year', fontsize=20)
ax1.tick_params(axis='x', rotation=0, labelsize=12)
ax1.set_ylabel('Personal Savings Rate', color='tab:red', fontsize=20)
ax1.tick_params(axis='y', rotation=0, labelcolor='tab:red')
ax1.grid(alpha=.4)
# ax2(右 Y 轴)
ax2.set_ylabel("# Unemployed (1000's)", color='tab:blue', fontsize=20)
ax2.tick_params(axis='y', labelcolor='tab:blue')
ax2.set_xticks(np.arange(0, len(x), 60))
ax2.set_xticklabels(x[::60], rotation=90, fontdict={'fontsize': 10})
ax2.set_title("Personal Savings Rate vs Unemployed", fontsize=222)
fig.tight_layout()
plt.show()
上述代码绘制了两个数据系列的折线图,分别位于左右 Y 轴上。其中,左 Y 轴对应个人储蓄率(Personal Savings Rate),右 Y 轴对应失业人数(Unemployed)。图表还添加了适当的标签、刻度和标题,并使用不同颜色区分了两个数据系列。输出的结果如下图所示。
图 7 双Y轴图
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: