polyfit在matlab中的用法(附带实例)
在 MATLAB 中,函数 polyfit() 采用最小二乘法对给定的数据进行多项式拟合,得到该多项式的系数。
polyfit() 函数的调用格式如下:
【实例】某数据的横坐标为 [0.3 0.4 0.7 0.9 1.2 1.9 2.8 3.2 3.7 4.5],纵坐标为 [1 2 3 4 5 2 6 9 2 7],对该数据进行多项式拟合。在编辑器窗口中依次输入:
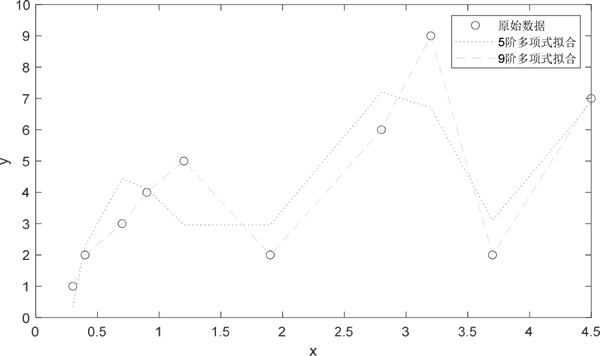
图 1 多项式曲线拟合结果
由上图可以看出,在使用 5 阶多项式拟合时,拟合效果比较差。
当采用 9 阶多项式拟合时,得到的拟合结果与原始数据比较相符。当使用函数 polyfit() 进行拟合时,多项式的阶次最大不超过 length(x)-1。
polyfit() 函数的调用格式如下:
- polyfit(x, y, n):找到次数为 n 的多项式系数,对于数据集合{(xi, yi)},满足差的平方和最小。
- [p, E]=polyfit(x, y, n):返回同上的多项式系数 p 和矩阵 E。多项式系数在向量 p 中,矩阵 E 用在 polyval() 函数中以计算误差。
【实例】某数据的横坐标为 [0.3 0.4 0.7 0.9 1.2 1.9 2.8 3.2 3.7 4.5],纵坐标为 [1 2 3 4 5 2 6 9 2 7],对该数据进行多项式拟合。在编辑器窗口中依次输入:
clear all
x=[0.3 0.4 0.7 0.9 1.2 1.9 2.8 3.2 3.7 4.5];
y=[1 2 3 4 5 2 6 9 2 7];
p5=polyfit(x,y,5); %5阶多项式拟合
y5=polyval(p5,x);
p5=vpa(poly2sym(p5),5) %显示5阶多项式
p9=polyfit(x,y,9); %9阶多项式拟合
y9=polyval(p9,x);
figure; %画图显示
plot(x,y,'bo');
hold on;
plot(x,y5,'r:');
plot(x,y9,'g--');
legend('原始数据','5阶多项式拟合','9阶多项式拟合');
xlabel('x');
ylabel('y');
运行程序后,得到的 5 阶多项式如下:
p5 =
0.8877*x^5 - 10.3*x^4 + 42.942*x^3 - 77.932*x^2 + 59.833*x - 11.673

图 1 多项式曲线拟合结果
由上图可以看出,在使用 5 阶多项式拟合时,拟合效果比较差。
当采用 9 阶多项式拟合时,得到的拟合结果与原始数据比较相符。当使用函数 polyfit() 进行拟合时,多项式的阶次最大不超过 length(x)-1。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: