直接插入排序算法(Java实现)
直接插入排序的基本思想是,假设前 i-1 个元素已经有序,将第 i 个元素的关键字与前 i-1 个元素的关键字进行比较,找到合适的位置,将第 i 个元素插入。按照类似的方法,将剩下的元素依次插入已经有序的序列中,完成插入排序。
假设待排序的元素有 n 个,对应的关键字分别是 a1,a2,…,an,因为第 1 个元素是有序的,所以从第 2 个元素开始,将 a2 与 a1 进行比较。若 a2 < a1,则将 a2 插入 a1 之前,否则说明已经有序,不需要移动 a2。
这样,有序的元素个数变为 2,然后将 a3 与 a2、a1 进行比较,确定 a3 的位置。首先将 a3 与 a2 进行比较:
以此类推,直到最后一个关键字 an 插入前 n-1 个有序序列。
例如,给定一个含有 8 个元素的序列,对应的关键字序列为 (45,23,56,12,97,76,29,68),将这些元素按照关键字从小到大进行直接插入排序的过程如下图所示。
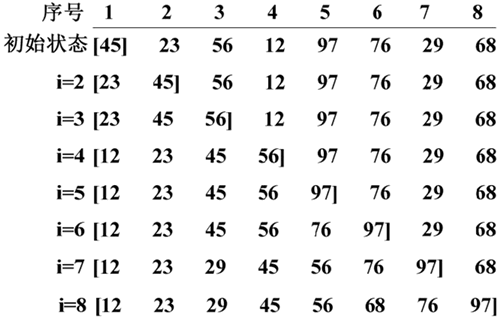
图 1 直接插入排序的过程
直接插入排序算法描述如下:
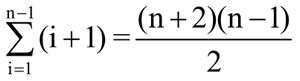
移动次数为:
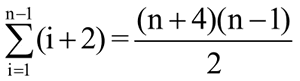
即在最坏的情况下的时间复杂度为 O(n^2)。
若元素的关键字是随机排列的,其比较次数和移动次数约为 n^2/4,此时直接插入排序算法的时间复杂度为 O(n^2),直接插入排序算法的空间复杂度为 O(1)。直接插入排序是一种稳定的排序算法。
假设待排序的元素有 n 个,对应的关键字分别是 a1,a2,…,an,因为第 1 个元素是有序的,所以从第 2 个元素开始,将 a2 与 a1 进行比较。若 a2 < a1,则将 a2 插入 a1 之前,否则说明已经有序,不需要移动 a2。
这样,有序的元素个数变为 2,然后将 a3 与 a2、a1 进行比较,确定 a3 的位置。首先将 a3 与 a2 进行比较:
- 若 a3≥a2,则说明 a1、a2、a3 已经有序排列;
- 若 a3<a2,则继续将 a3 与 a1 比较。若 a3<a1,则将 a3 插入 a1 之前,否则将 a3 插入 a1 与 a2 之间,即可完成 a1、a2、a3 的排列。
以此类推,直到最后一个关键字 an 插入前 n-1 个有序序列。
例如,给定一个含有 8 个元素的序列,对应的关键字序列为 (45,23,56,12,97,76,29,68),将这些元素按照关键字从小到大进行直接插入排序的过程如下图所示。

图 1 直接插入排序的过程
直接插入排序算法描述如下:
public void DirectInsertSort()
// 直接插入排序
{
int i = 0, t = -1, j = 0;
for (i = 0; i < length - 1; i++) // 前 i 个元素已经有序,从第 i + 1 个元素开始与前 i 个有序的关键字进行比较
{
t = data[i + 1]; // 取出第 i + 1 个元素,即待排序的元素
j = i;
while (j > -1 && t < data[j]) // 寻找当前元素的合适位置
{
data[j + 1] = data[j];
j--;
}
data[j + 1] = t; // 将当前元素插入合适的位置
}
}
从上面的算法可以看出,直接插入排序算法简单且容易实现。在最好的情况下,即所有元素的关键字已经基本有序,直接插入排序算法的时间复杂度为 O(n)。在最坏的情况下,即所有元素的关键字都是按逆序排列的,内层 while 循环的比较次数均为 i+1,整个比较次数为: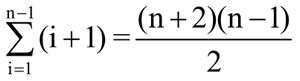
移动次数为:
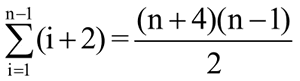
即在最坏的情况下的时间复杂度为 O(n^2)。
若元素的关键字是随机排列的,其比较次数和移动次数约为 n^2/4,此时直接插入排序算法的时间复杂度为 O(n^2),直接插入排序算法的空间复杂度为 O(1)。直接插入排序是一种稳定的排序算法。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: