C++ std::stack的使用(新手必看)
栈(stack)是一种遵循 FILO(First In Last Out,先进后出)原则的数据结构。它通过两个主要的接口操作元素,并提供多种方式访问栈顶元素、查询栈的大小以及判断栈是否为空。
在 C++ 中,借助 STL(标准模板库),我们可以便捷地实现和使用栈这一数据结构。
栈是一种线性数据结构,可被视为一种“功能受限”的数组。栈只允许在栈顶进行数据操作,栈内的其他元素无法被直接访问。这种限制性赋予了栈独特的特性,例如在深度优先搜索(DFS)中,结点的遍历顺序与栈的结构紧密相关,如下图所示。
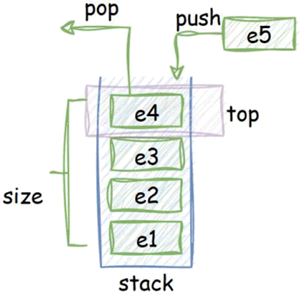
图 1 栈的结构
通常情况下,我们声明一个空栈,然后向其中添加元素。示例代码如下:
在使用 top() 方法之前,务必确保栈非空,否则可能导致运行时错误(RE)。
判断栈是否为空的方法有两种:
需要注意的是,stack 没有提供 clear() 方法来清空栈。如需清空栈,可以使用以下代码:
【实例】 StarryCoding P38火车轨道。
给定 n 列火车,每列火车具有一个唯一的编号,编号的取值范围为 1~n(这些编号形成了一个特定的排列)。
目前,这些火车按照一定的顺序停在一条轨道上,并且可以在两个方向上移动。我们需要判断是否可以通过一个车站,而且每列火车最多只进站一次,使得它们离开车站时的编号顺序是升序的。
该车站采用栈的数据结构,位于输入队列轨道的中间位置,形成了一个T字形状的结构。初始状态下,所有火车都停靠在车站的右侧。
如果可以达到上述目标,则输出 Yes;否则,输出 No。
输入格式:
输出格式:
样例输入:
样例输入:
解题思路:为了模拟车站的功能,我们使用一个栈结构。首先,确定当前应当出站的火车编号(即按照升序排列的编号)。接着,依次让火车进站。当栈顶的火车恰好是当前应该出站的编号时,这列火车便出站。这一过程持续进行,直到所有火车都有机会进站和出站。
最后,检查栈内是否还有剩余的火车。如果栈为空,则意味着所有火车都已正确出站,并且它们的编号是按升序排列的,因此可以输出 Yes。反之,如果栈内仍然有火车,则说明无法通过单次进站使火车编号排列成升序,此时应输出 No。
C++实现程序如下:
在 C++ 中,借助 STL(标准模板库),我们可以便捷地实现和使用栈这一数据结构。
栈是一种线性数据结构,可被视为一种“功能受限”的数组。栈只允许在栈顶进行数据操作,栈内的其他元素无法被直接访问。这种限制性赋予了栈独特的特性,例如在深度优先搜索(DFS)中,结点的遍历顺序与栈的结构紧密相关,如下图所示。

图 1 栈的结构
C++ stack初始化
在使用栈之前,需要引入相应的头文件。如果已经引入了万能头文件(<bits/stdc++.h>),则无须额外引入栈头文件。示例代码如下:#include <stack> // #include <bits/stdc++.h> // 如果使用万能头文件,则包含栈 using namespace std; // stack位于std命名空间中声明一个栈时,使用 stack<T> 的形式,其中T代表数据类型,可以是 int、double、char 等,也可以是自定义的结构体。但需要注意,一个栈内的所有元素必须具有相同的数据类型。
通常情况下,我们声明一个空栈,然后向其中添加元素。示例代码如下:
stack<T> stk; // T为数据类型 stack<int> stk_int; // 声明一个存储int类型元素的栈
C++ stack基本操作
栈提供了一些基本操作方法来管理栈内的元素,如下表所示。| 方法 | 作用 | 时间复杂度 |
|---|---|---|
| push(x) | 将元素x推入栈顶 | O(1) |
| pop() | 弹出栈顶元素,但不会返回该元素 | O(1) |
| top() | 返回栈顶元素,但不会弹出该元素 | O(1) |
| size() | 返回栈中的元素个数 | O(1) |
| empty() | 判断栈是否为空 | O(1) |
在使用 top() 方法之前,务必确保栈非空,否则可能导致运行时错误(RE)。
判断栈是否为空的方法有两种:
//方法一:用empty()方法判断 cout << (stk.empty() ? "栈为空" : "栈非空") << '\n'; //方法二:用size()方法判断 cout << (stk.size() ? "栈非空" : "栈为空") << '\n';
需要注意的是,stack 没有提供 clear() 方法来清空栈。如需清空栈,可以使用以下代码:
while(!stk.empty()) stk.pop();
【实例】 StarryCoding P38火车轨道。
给定 n 列火车,每列火车具有一个唯一的编号,编号的取值范围为 1~n(这些编号形成了一个特定的排列)。
目前,这些火车按照一定的顺序停在一条轨道上,并且可以在两个方向上移动。我们需要判断是否可以通过一个车站,而且每列火车最多只进站一次,使得它们离开车站时的编号顺序是升序的。
该车站采用栈的数据结构,位于输入队列轨道的中间位置,形成了一个T字形状的结构。初始状态下,所有火车都停靠在车站的右侧。
如果可以达到上述目标,则输出 Yes;否则,输出 No。
输入格式:
- 第一行包含一个整数 n(1≤n≤105)。
- 第二行包含 n 个整数 ai,表示在进站口的火车编号(1≤ai≤n,ai≠aj)。
输出格式:
- 如果火车编号可以变为升序,则输出 Yes;否则,输出 No。
样例输入:
3
3 1 2
Yes
样例输入:
4
3 4 1 2
No
解题思路:为了模拟车站的功能,我们使用一个栈结构。首先,确定当前应当出站的火车编号(即按照升序排列的编号)。接着,依次让火车进站。当栈顶的火车恰好是当前应该出站的编号时,这列火车便出站。这一过程持续进行,直到所有火车都有机会进站和出站。
最后,检查栈内是否还有剩余的火车。如果栈为空,则意味着所有火车都已正确出站,并且它们的编号是按升序排列的,因此可以输出 Yes。反之,如果栈内仍然有火车,则说明无法通过单次进站使火车编号排列成升序,此时应输出 No。
C++实现程序如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;
int a[N];
signed main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n; cin >> n;
for (int i = 1; i <= n; ++ i) cin >> a[i];
stack<int> stk;
// 车站,存放的是火车编号
int pt = 1;
// pt为当前车站外等待入站的车的下标
bool ans = true;
// 初始化答案为true
for (int i = 1; i <= n; ++ i){
// 当车站内为空或栈顶的火车编号并非当前想要出站的编号时,继续进一列火车
while (stk.empty() || (pt <= n && stk.top() != i)) stk.push(a[pt ++]);
// 如果当前火车可以出站,就直接出站,如果不行,则说明答案为false
if (stk.size() && stk.top() == i) stk.pop();
else ans = false;
}
cout << (ans ? "Yes" : "No") << '\n';
return 0;
}
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: