原码、反码、补码及位操作符,C语言位操作详解
计算机中的所有数据均是以二进制形式存储和处理的。所谓位操作就是直接把计算机中的二进制数进行操作,无须进行数据形式的转换,故处理速度较快。
字节(Byte)是计算机处理数据的基本单位,通常系统中一个字节为 8 位。即:1 Byte=8 bit。
为便于演示,本节表示的原码、反码及补码均默认为 8 位。
准确地说,数据在计算机中是以其补码形式存储和运算的。在介绍补码之前,先了解原码和反码的概念。
正数的原码、反码、补码均相同。
原码:用最高位表示符号位,其余位表示数值位的编码称为原码。其中,正数的符号位为 0,负数的符号位为 1。
负数的反码:把原码的符号位保持不变,数值位逐位取反,即可得原码的反码。
负数的补码:在反码的基础上加 1 即得该原码的补码。
例如:
+11 的原码为: 0000 1011
+11 的反码为: 0000 1011
+11 的补码为: 0000 1011
-7 的原码为:1000 0111
-7 的反码为:1111 1000
-7 的补码为:1111 1001
注意,对补码再求一次补码操作就可得该补码对应的原码。
注意,计算机中位运算操作,均是以二进制补码形式进行的。
例如,计算 20 和 9 按位与的结果,如下所示。

即:20&9=0。
应用一:使用 0x01 与一个数按位与,可获取该数对应二进制数的最低位。
应用二:使用 0x00 与一个数按位与,可使该数低位的一个字节清零。
例如,9&0x1 可求得 9 对应二进制数 0000 1001 的最低位 1。
【例 1】分析以下程序的功能,并输出其运行结果。
2 4 6 8 10 12 14 16 18 20
程序分析:
n&0x1 的功能是取出 n 对应补码二进制数的最低位(最右端位),如果该位为 0,则输出。二进制数 bn-1bn-2bn-3…b2b1b0。对应的十进制数 N 的表达式为:
例如,计算 20 和 9 按位或的结果,如下所示。

即: 20 | 9 = 29。
复合赋值运算符:
例如,计算 22 和 7 按位异或的结果,如下所示。

即:22^7=17。
【例 2】分析以下程序的功能。
a=5,b=3
程序分析:
本题是对按位异或的性质和特点的综合运用,由于没有使用中间变量,故在理解上存在一定的难度。
由于 a=a^b; 故:
b=a^b=a^b^b=a^(b^b)=a^0=a,即:b=3。
a=a^b=(a^b)^a=(b^a)^a=b^(a^a)=b^0=b,即:a=5。
故实现了 a 与 b 的交换。
复合赋值运算符:
例如,计算 10 左移两位的结果,如下所示。
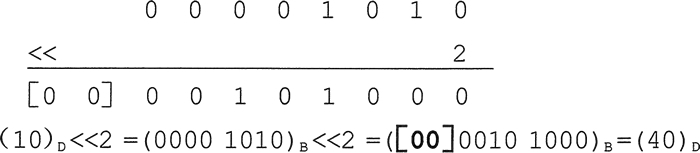
丢弃左边高位移出去的 0,低位补 0。
左移一位相当于该数乘以 2,本例中左移两位,故相当于乘以 4。即:10<<2 = 10 X 2 X 2 = 40。
复合赋值运算符:
例如,计算 70 右移两位的结果,如下所示。
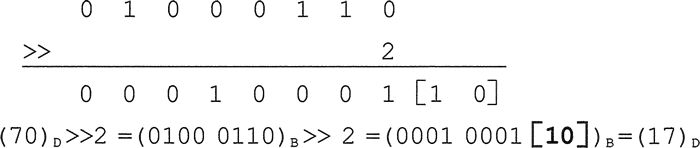
丢弃右边移出去的所有位,由于该数为正数,左边补 0。
右移一位相当于该数除以 2 取整,本例中右移两位,故相当于除以 4 取整。即:70>>2=70/4 = 17。
例如,计算 10 按位取反的结果,如下所示:
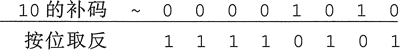
由于计算机中位运算均是以补码形式操作的,正数的补码是其本身,负数的补码为其反码加 1。
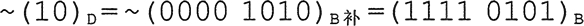
所得显然是负数的补码,对补码 1111 0101 再做一次求补操作,即可得该补码对应的原码。 求 1111 0101 补码的过程如下所示。
原码、反码和补码
位(bit)是计算机中处理数据的最小单位,其取值只能是 0 或 1。字节(Byte)是计算机处理数据的基本单位,通常系统中一个字节为 8 位。即:1 Byte=8 bit。
为便于演示,本节表示的原码、反码及补码均默认为 8 位。
准确地说,数据在计算机中是以其补码形式存储和运算的。在介绍补码之前,先了解原码和反码的概念。
正数的原码、反码、补码均相同。
原码:用最高位表示符号位,其余位表示数值位的编码称为原码。其中,正数的符号位为 0,负数的符号位为 1。
负数的反码:把原码的符号位保持不变,数值位逐位取反,即可得原码的反码。
负数的补码:在反码的基础上加 1 即得该原码的补码。
例如:
+11 的原码为: 0000 1011
+11 的反码为: 0000 1011
+11 的补码为: 0000 1011
-7 的原码为:1000 0111
-7 的反码为:1111 1000
-7 的补码为:1111 1001
注意,对补码再求一次补码操作就可得该补码对应的原码。
位操作符
语言中提供了 6 个基本的位操作符,如表 2 所示。| 运算符 | 功 能 | 运算规则 |
|---|---|---|
| & | 按位与 | 对应位均为 1 时,结果才为 1 |
| | | 按位或 |
两位中只要有一位为 1,结果为 1。 只有两位同时为 0 时,结果为才为 0。 |
| ^ | 按位异或 | 两位相异时,结果为 1;两位相同时,结果为 0。 |
| << | 左移 | 将运算数的各二进制位均左移若干位,高位丢弃(不包括 1),低位补 0,每左移一位,相当于该数乘以 2。 |
| >> | 右移 | 将运算数的各二进制位均右移若干位,正数补左补 0,负数左补 1,右边移出的位丢弃。 |
| ~ | 按位取反 | 0 变 1,1 变 0。 |
注意,计算机中位运算操作,均是以二进制补码形式进行的。
按位与(&)
只有两位同时为 1 时,结果才为 1;只要两位中有一位为 0,则结果为 0。用式子表示为:
0 & 0 = 0
0 & 1 = 0
1 & 0 = 0
1 & 1 = 1
&= 表示按位与后赋值。例如,计算 20 和 9 按位与的结果,如下所示。

即:20&9=0。
应用一:使用 0x01 与一个数按位与,可获取该数对应二进制数的最低位。
应用二:使用 0x00 与一个数按位与,可使该数低位的一个字节清零。
例如,9&0x1 可求得 9 对应二进制数 0000 1001 的最低位 1。
【例 1】分析以下程序的功能,并输出其运行结果。
#include<stdio.h>
int main (void)
{
int n;
for(n=1;n<=20;n++)
if (0==(n&0x1))
printf("%d ",n);
printf ("\n");
return 0;
}
程序运行结果为:2 4 6 8 10 12 14 16 18 20
程序分析:
n&0x1 的功能是取出 n 对应补码二进制数的最低位(最右端位),如果该位为 0,则输出。二进制数 bn-1bn-2bn-3…b2b1b0。对应的十进制数 N 的表达式为:
N=b0 X 20 + b1 X 21 + b2 X 22 + b3 X 23 + b4 X 24 + …
由于从上式中第二项开始的每一项都是偶数,故N是否偶数取决于 b0 是否偶数,故 b0 为 1 时是奇数,为 0 时是偶数。按位或(丨)
只要两位中有一位为 1,结果为 1;只有两位同时为 0 时,结果才为 0。用式子表示为:
0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1
|= 按位或后赋值。例如,计算 20 和 9 按位或的结果,如下所示。

即: 20 | 9 = 29。
按位异或(^)
当两位相同时,即同为 1 或同为 0 时,结果为 0;当两位相异时,即其中一位为 1,另一位为 0 时,结果为 1。即相同为 0,相异为 1。用式子表示为:
0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 0
- a^0=a。即0与任意数按位异或都得该数本身。
- 1 与任意二进制位按位异或都得该位取反(0 变 1,1 变 0)。
- a^a=0。即任意数与自身按位异或都得0。
- a^b=b^a。即满足交换律。
- (a^b)^c=a^(b^c)。即满足结合律。
- a^b^b=a^(b^b)=a^0=a。
复合赋值运算符:
^= 按位异或后赋值。例如,计算 22 和 7 按位异或的结果,如下所示。

即:22^7=17。
【例 2】分析以下程序的功能。
#include<stdio.h>
int main (void)
{
int a=3,b=5;
a=a^b;
b=a^b;
a=a^b;
printf("a=%d,b=%d\n",a,b);
return 0;
}
运行结果:a=5,b=3
程序分析:
本题是对按位异或的性质和特点的综合运用,由于没有使用中间变量,故在理解上存在一定的难度。
由于 a=a^b; 故:
b=a^b=a^b^b=a^(b^b)=a^0=a,即:b=3。
a=a^b=(a^b)^a=(b^a)^a=b^(a^a)=b^0=b,即:a=5。
故实现了 a 与 b 的交换。
左移(<<)
将运算数的各二进制位均左移若干位,高位丢弃(不包含 1),低位补 0。左移时舍弃的高位不包含 1,则每左移一位,相当于该数乘以 2。复合赋值运算符:
<<= 左移后赋值。例如,计算 10 左移两位的结果,如下所示。
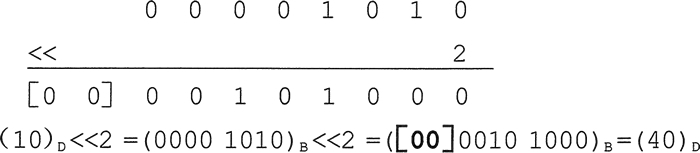
丢弃左边高位移出去的 0,低位补 0。
左移一位相当于该数乘以 2,本例中左移两位,故相当于乘以 4。即:10<<2 = 10 X 2 X 2 = 40。
右移(>>)
将运算数的各二进制位全部右移若干位,正数左补 0,负数左补 1,右边移出的位丢弃。复合赋值运算符:
>>= 右移后赋值。例如,计算 70 右移两位的结果,如下所示。
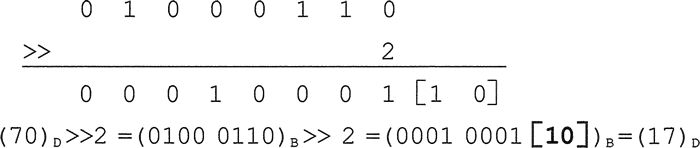
丢弃右边移出去的所有位,由于该数为正数,左边补 0。
右移一位相当于该数除以 2 取整,本例中右移两位,故相当于除以 4 取整。即:70>>2=70/4 = 17。
按位取反(~)
0 变 1,1 变 0。用式子表示为:
~0 = 1
~1 = 0
例如,计算 10 按位取反的结果,如下所示:
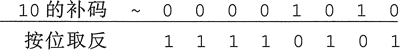
由于计算机中位运算均是以补码形式操作的,正数的补码是其本身,负数的补码为其反码加 1。
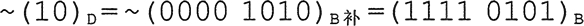
所得显然是负数的补码,对补码 1111 0101 再做一次求补操作,即可得该补码对应的原码。 求 1111 0101 补码的过程如下所示。
反码 1000 1010 --符号位 1 保持不变,数值位按位取反
补码 1000 1011 --反码加1
根据 (补码)补码=原码
故补码1111 0101对应的原码为1000 1011=-11,即:~(10)D =~(0100 0110)B补= (1111 0101)B补=-11
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: