NumPy矩阵加减乘除运算详解(附带实例)
如果两个矩阵大小相同,我们可以使用算术运算符“+”、“-”、“*”和“/”对矩阵进行加、减、乘、除运算。
【实例 1】创建两个矩阵 data1 和 data2,实现矩阵的加法运算,效果如下图所示:
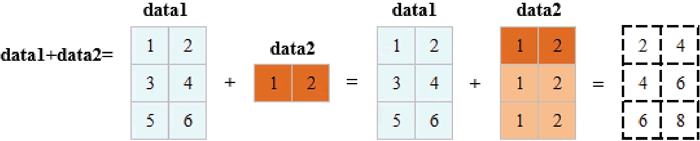
图 1 矩阵加法运算示意图
程序代码如下:
【实例 2】除了加法运算,还可以实现矩阵的减法、乘法和除法运算。接下来先实现上述矩阵的减法和除法运算,程序代码如下:
当我们对上述矩阵进行乘法运算时,程序出现了错误,原因是矩阵的乘法运算要求左边矩阵的列数和右边矩阵的行数要一致。由于上述矩阵 data2 只有一行,所以导致程序出错。
【实例 3】将矩阵 data2 改为 2×2 的矩阵,再进行矩阵的乘法运算,程序代码如下:

图 2 矩阵相乘的运算过程
例如,1×1+2×3=7,是第一个矩阵第 1 行元素与第二个矩阵第 1 列元素两两相乘并求和得到的。
数组运算和矩阵运算的一个关键区别是矩阵相乘使用的是点乘。点乘也称点积,是数组中元素对应位置一一相乘之后求和的操作,在 NumPy 中专门提供了点乘方法,即 dot() 方法。
【实例 4】数组相乘与数组点乘运算,程序代码如下:
【实例 5】要实现矩阵对应元素之间相乘可以使用 multiply() 函数,程序代码如下:
【实例 1】创建两个矩阵 data1 和 data2,实现矩阵的加法运算,效果如下图所示:

图 1 矩阵加法运算示意图
程序代码如下:
import numpy as np # 导入numpy模块
data1 = np.mat('1 2; 3 4; 5 6') # 创建矩阵
data2 = np.mat([1, 2])
print(data1 + data2) # 矩阵加法运算
运行程序,结果如下:
[[2 4]
[4 6]
[6 8]]
【实例 2】除了加法运算,还可以实现矩阵的减法、乘法和除法运算。接下来先实现上述矩阵的减法和除法运算,程序代码如下:
import numpy as np # 导入numpy模块
data1 = np.mat('1 2; 3 4; 5 6') # 创建矩阵
data2 = np.mat([1, 2])
print(data1 - data2) # 矩阵减法运算
print(data1 / data2) # 矩阵除法运算
运行程序,结果如下:
[[0 0]
[2 2]
[4 4]]
[[1. 1.]
[3. 2.]
[5. 3.]]
当我们对上述矩阵进行乘法运算时,程序出现了错误,原因是矩阵的乘法运算要求左边矩阵的列数和右边矩阵的行数要一致。由于上述矩阵 data2 只有一行,所以导致程序出错。
【实例 3】将矩阵 data2 改为 2×2 的矩阵,再进行矩阵的乘法运算,程序代码如下:
import numpy as np # 导入numpy模块
data1 = np.mat('1 2; 3 4; 5 6') # 创建矩阵
data2 = np.mat('1 2; 3 4')
print(data1 * data2) # 矩阵乘法运算
运行程序,结果如下:
[[ 7 10]
[15 22]
[23 34]]

图 2 矩阵相乘的运算过程
例如,1×1+2×3=7,是第一个矩阵第 1 行元素与第二个矩阵第 1 列元素两两相乘并求和得到的。
数组运算和矩阵运算的一个关键区别是矩阵相乘使用的是点乘。点乘也称点积,是数组中元素对应位置一一相乘之后求和的操作,在 NumPy 中专门提供了点乘方法,即 dot() 方法。
【实例 4】数组相乘与数组点乘运算,程序代码如下:
import numpy as np # 导入numpy模块
n1 = np.array([1, 2, 3]) # 创建数组
n2 = np.array([[1, 2, 3], [1, 2, 3], [1, 2, 3]])
print("数组相乘结果为:\n", n1 * n2) # 数组相乘
print("数组点乘结果为:\n", np.dot(n1, n2)) # 数组点乘
运行程序,结果如下:
数组相乘结果为:
[[1 4 9]
[1 4 9]
[1 4 9]]
数组点乘结果为:
[ 6 12 18]
【实例 5】要实现矩阵对应元素之间相乘可以使用 multiply() 函数,程序代码如下:
import numpy as np # 导入numpy模块
n1 = np.mat('1 3 3; 4 5 6; 7 12 9') # 创建矩阵,使用分号隔开数据
n2 = np.mat('2 6 6; 8 10 12; 14 24 18')
print("矩阵相乘结果为:\n", n1 * n2) # 矩阵相乘
print("矩阵对应元素相乘结果为:\n", np.multiply(n1, n2))
运行程序,结果如下:
矩阵相乘结果为:
[[ 68 108 96]
[132 218 192]
[236 378 348]]
矩阵对应元素相乘结果为:
[[ 2 18 18]
[ 32 50 72]
[ 98 288 162]]
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: