Kruskal克鲁斯卡尔算法求最小生成树(Java实现)
最小生成树是指在一个连通网的所有生成树中,其中所有边的代价之和最小的那棵生成树。代价在网中通过权值来表示,一棵生成树的代价就是生成树各边的代价之和。
例如要在 n 个城市建立一个交通图,就是要在 n(n-1)/2 条线路中选择 n-1 条代价最小的线路,各个城市可以看成是图的顶点,城市的线路可以看作图的边。
最小生成树具有一个重要的性质,假设一个连通网 N=(V,E),V 是顶点的集合,E 是边的集合,V 有一个非空子集 U。如果 (u,v) 是一条具有最小权值的边,其中 u∈U、v∈V-U,那么一定存在一个最小生成树包含边 (u,v)。
下面用反证法证明以上性质。假设所有的最小生成树都不存在这样的一条边 (u,v)。设 T 是连通网 N 中的一棵最小生成树,如果将边 (u,v) 加入 T 中,那么根据生成树的定义,T 一定出现包含 (u,v) 的回路。另外,T 中一定存在一条边 (u',v') 的权值大于或等于 (u,v) 的权值,若删除边 (u',v'),则得到一棵代价小于或等于 T 的生成树 T'。T' 是包含边 (u,v) 的最小生成树,这与假设矛盾。由此,以上性质得证。
最小生成树的构造算法有两个,分别是 Prim(普里姆)算法和 Kruskal(克鲁斯卡尔)算法,本节重点讲解 Kruskal 算法。
例如利用 Kruskal 算法构造最小生成树的过程,如下图所示:
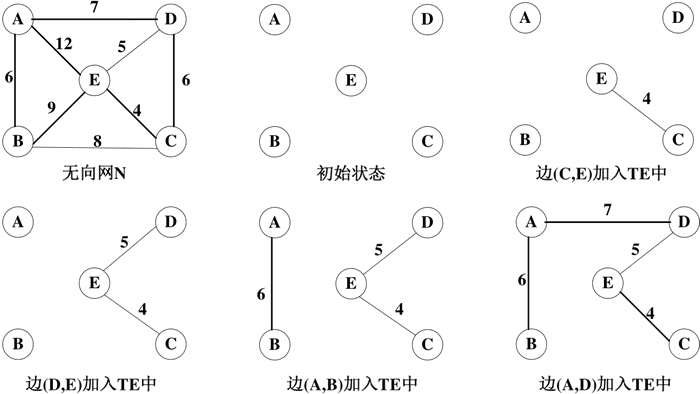
图 1 Kruskal算法构造最小生成树的过程
初始时,边的集合 TE 为空集,顶点 A、B、C、D、E 分别属于不同的集合,假设 U1={A}、U2={B}、U3={C}、U4={D}、U5={E}。图中含有 8 条边,将这 8 条边按照权值从小到大排列,依次取出最小的边,若依附于边的两个顶点属于不同的结合,则将该边加入集合 TE 中,并将这两个顶点合并为一个集合,重复执行类似操作,直到所有顶点都属于一个集合为止。
在这 8 条边中,权值最小的边是 (C,E),其权值 cost(C,E)=4,并且 C∈U3、E∈U5、U3≠U5,因此,将边 (C,E) 加入集合 TE 中,并将两个顶点集合合并为一个集合,TE={(C,E)}、U3=U5={C,E}。
在剩下的边的集合中,边 (D,E) 的权值最小,其权值 cost(D,E)=5,并且 D∈U4、E∈U3、U3≠U4,因此将边 (D,E) 加入边的集合TE中并合并顶点集合,有 TE={(C,E),(D,E)}、U3=U5=U4={C,E,D}。
然后继续从剩下的边的集合中选择权值最小的边,依次加入 TE 中,合并顶点集合,直到所有的顶点都加入顶点集合。
Kruskal 算法描述如下:
例如要在 n 个城市建立一个交通图,就是要在 n(n-1)/2 条线路中选择 n-1 条代价最小的线路,各个城市可以看成是图的顶点,城市的线路可以看作图的边。
最小生成树具有一个重要的性质,假设一个连通网 N=(V,E),V 是顶点的集合,E 是边的集合,V 有一个非空子集 U。如果 (u,v) 是一条具有最小权值的边,其中 u∈U、v∈V-U,那么一定存在一个最小生成树包含边 (u,v)。
下面用反证法证明以上性质。假设所有的最小生成树都不存在这样的一条边 (u,v)。设 T 是连通网 N 中的一棵最小生成树,如果将边 (u,v) 加入 T 中,那么根据生成树的定义,T 一定出现包含 (u,v) 的回路。另外,T 中一定存在一条边 (u',v') 的权值大于或等于 (u,v) 的权值,若删除边 (u',v'),则得到一棵代价小于或等于 T 的生成树 T'。T' 是包含边 (u,v) 的最小生成树,这与假设矛盾。由此,以上性质得证。
最小生成树的构造算法有两个,分别是 Prim(普里姆)算法和 Kruskal(克鲁斯卡尔)算法,本节重点讲解 Kruskal 算法。
Kruskal算法
Kruskal 算法的基本思想是:假设 N={V,E} 是连通网,TE 是 N 的最小生成树的边的集合。执行以下操作:- 初始时,最小生成树中只有 n 个顶点,这 n 个顶点分别属于不同的集合,而边的集合 TE=ϕ;
- 从连通网 N 中选择一个代价最小的边,若边所依附的两个顶点在不同的集合中,则将该边加入最小生成树 TE 中,并将该边依附的两个顶点合并到同一个集合中;
- 重复执行第二个步骤,直到所有的顶点都属于同一个顶点集合为止。
例如利用 Kruskal 算法构造最小生成树的过程,如下图所示:

图 1 Kruskal算法构造最小生成树的过程
初始时,边的集合 TE 为空集,顶点 A、B、C、D、E 分别属于不同的集合,假设 U1={A}、U2={B}、U3={C}、U4={D}、U5={E}。图中含有 8 条边,将这 8 条边按照权值从小到大排列,依次取出最小的边,若依附于边的两个顶点属于不同的结合,则将该边加入集合 TE 中,并将这两个顶点合并为一个集合,重复执行类似操作,直到所有顶点都属于一个集合为止。
在这 8 条边中,权值最小的边是 (C,E),其权值 cost(C,E)=4,并且 C∈U3、E∈U5、U3≠U5,因此,将边 (C,E) 加入集合 TE 中,并将两个顶点集合合并为一个集合,TE={(C,E)}、U3=U5={C,E}。
在剩下的边的集合中,边 (D,E) 的权值最小,其权值 cost(D,E)=5,并且 D∈U4、E∈U3、U3≠U4,因此将边 (D,E) 加入边的集合TE中并合并顶点集合,有 TE={(C,E),(D,E)}、U3=U5=U4={C,E,D}。
然后继续从剩下的边的集合中选择权值最小的边,依次加入 TE 中,合并顶点集合,直到所有的顶点都加入顶点集合。
Kruskal 算法描述如下:
public void Kruskal(MGraph M)
//Kruskal 算法求最小生成树
{
int set[] = new int[M.vexnum];
int a = 0, b = 0;
double min = M.arc[a][b];
int k = 0;
for (int i = 0; i < M.vexnum; i++) // 初始化,各顶点分别属于不同的集合
set[i] = i;
System.out.println("最小生成树的各条边为:");
while (k < M.vexnum - 1) // 查找所有最小权值的边
{
for (int i = 0; i < M.vexnum; i++) // 在矩阵的上三角查找最小权值的边
{
for (int j = i + 1; j < M.vexnum; j++) {
if (M.arc[i][j] < min) {
min = M.arc[i][j];
a = i;
b = j;
}
}
}
M.arc[a][b] = Double.POSITIVE_INFINITY; // 删除上三角中最小权值的边,下次不再查找
min = M.arc[a][b];
if (set[a] != set[b]) // 如果边的两个顶点在不同的集合
{
System.out.print("(" + M.vex[a] + "-" + M.vex[b] + ")" + "\n"); // 输出最小权值的边
k += 1;
for (int r = 0; r < M.vexnum; r++)
if (set[r] == set[b]) // 将顶点 b 所在集合并入顶点 a 所在集合中
set[r] = set[a];
}
}
}
最小生成树的各条边为:(C-E) (D-E) (A-B) (A-D)。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: