C++ sort()排序算法详解(附带实例)
在 C++ 中,排序算法多种多样,从简单的冒泡排序到复杂的希尔排序,每种算法都有其特定的应用场景和性能特点。然而,对于大多数应用来说,这些排序算法的实现可能过于复杂,而且效率也参差不齐。
幸运的是,STL 为我们提供了强大的 sort() 算法,它基于高效的排序算法实现,能够轻松应对各种排序需求。使用 STL 的 sort() 算法,我们无须深入了解各种排序算法的具体实现,就可以快速、高效地完成排序任务。
只要确定了排序的数据范围,默认情况下,sort() 算法就会将数据元素按照从小到大的顺序排序,至于具体的排序和数据的移动,就无须我们操心了,sort() 算法会处理好一切。
例如,要对前面汇总后的学生成绩进行排序,只需要一条语句即可完成:
默认情况下,sort() 算法处理后的数据是按照从小到大的顺序排列的。如果想按照从大到小的顺序排列数据,则可以在容器排序完成之后,调用 reverse() 算法将容器中的所有数据翻转为逆序即可。例如:
例如,容器中保存的是自定义的表示矩形的 Rect 类型对象,我们希望按照矩形的面积对容器中的 Rect 对象进行排序,其代码如下:
在这个重载的运算符中,我们具体地定义了两个 Rect 对象比较的规则:首先计算两个矩形的面积,然后将两个面积比较的结果作为两个矩形比较的结果,也就是说,哪个矩形的面积大,就认为这个矩形大。
sort() 算法在对容器中的 Rect 对象进行排序时,会调用这个运算符对两个 Rect 对象进行大小比较,以此决定它们之间的先后顺序。
对容器中的数据进行排序,不仅仅是让数据按照某种顺序排列这么简单,更多时候,我们还会在容器中的数据排序完成后,对数据进行进一步的处理,以获得更多、更丰富的结果。
例如,针对排序完成的容器,可以使用 lower_bound() 算法和 upper_bound() 算法来获得容器中小于某个值或者大于某个值的临界点位置;可以使用 equal_range() 算法获得容器中所有等于某个值的数据范围。
可以说,使用 sort() 算法对容器中的数据进行排序是后续这些算法的前提,而这些算法又扩展了 sort() 算法的结果。两者相互配合使用,可以“优雅”地完成一些常见的数据处理任务。
以前文的学生成绩汇总的例子为例,当使用 sort() 算法对保存在 vecScore 容器中的汇总成绩排序完成后,我们还可以统计所有及格的学生总人数和刚好及格的学生人数,代码如下:
实际上,STL 提供了 count() 算法和 count_if() 算法,它们专门用于统计容器中符合某个条件的数据的数量。使用这两个算法,我们可以以一种更直接和优雅的方式进行计数:
在默认情况下,sort() 算法使用“<”关系运算符进行大小比较,并按照从小到大的顺序进行排序。虽然 sort() 算法的这种默认排序方式可以满足大多数需求,但在一些特殊情况下,我们希望按照某些特殊的方式对数据进行排序,即采用自定义的排序规则。
这时,我们就需要用到 sort() 算法的第二个版本,它的原型如下:
comp 参数可以接受一个函数,该函数用于定义排序的比较规则,因此它也被称为比较函数。比较函数有两个输入参数,它们是要进行比较的数据对应的数据类型,该函数还有一个 bool 类型的返回值。
sort()算法在执行时,会将容器中两个待比较的数据作为实际参数调用这个比较函数进行大小比较。在比较函数中,我们可以自定义比较规则,按照我们需要的方式来比较两个数据的大小,并最终返回一个 bool 值来表示这两个数据的大小关系。sort() 算法会根据这个大小关系来确定它们最终在容器中的先后顺序。
例如,可以利用 sort() 算法中的比较函数重新定义 vecRect 容器中 Rect 对象的排序规则,让它们按照矩形的长进行排序:
取而代之的事,sort() 算法会调用我们自定义的比较函数来完成对数据的比较。因为可以完全控制比较函数的实现,所以我们可以将特殊的比较规则融入到比较函数中,让 sort() 算法采用我们自定义的比较规则。
自定义比较规则还带来另一个好处,那就是实现比较规则的多样化。例如,如果某天老板心血来潮,希望让 Rect 对象按照矩形的宽进行排序,通过自定义 sort() 算法的比较规则,也能很快实现:
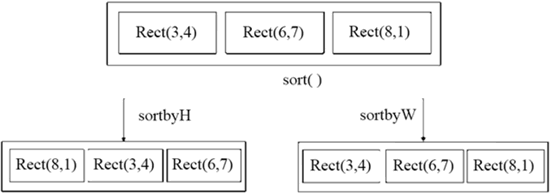
图 1 不同的比较函数,不同的比较结果
一般来说,sort() 算法提供的只是一个排序算法的框架,它负责维护整个排序过程。
例如,从容器中取出两个数据进行比较,并根据比较结果将数据放到容器的合适位置。但是,它将排序算法中最核心、最关键的部分—比较规则的定义,留给了我们。这样,我们可以自定义比较规则,使用相同的固定算法框架,应用不同的自定义比较规则来对不同类型的数据进行排序,从而实现排序算法的通用性和灵活性。
幸运的是,STL 为我们提供了强大的 sort() 算法,它基于高效的排序算法实现,能够轻松应对各种排序需求。使用 STL 的 sort() 算法,我们无须深入了解各种排序算法的具体实现,就可以快速、高效地完成排序任务。
C++ sort()的基本用法
sort() 算法的作用不小,但它的使用却非常简单,其函数原型如下:template <class RandomAccessIterator> void sort ( RandomAccessIterator first, RandomAccessIterator last );sort() 算法可以接受两个参数,分别用于指定需要进行排序的容器中数据的起始位置和结束位置。
只要确定了排序的数据范围,默认情况下,sort() 算法就会将数据元素按照从小到大的顺序排序,至于具体的排序和数据的移动,就无须我们操心了,sort() 算法会处理好一切。
例如,要对前面汇总后的学生成绩进行排序,只需要一条语句即可完成:
// 将vecScore容器中的学生成绩排序 sort(vecScore.begin(),vecScore.end());sort() 算法执行完成后,容器中的数据将按照从小到大的顺序排列。一个简单的函数调用就可以完成所有数据的排序工作,将程序员从复杂的冒泡排序、希尔排序等排序算法中解放出来。
默认情况下,sort() 算法处理后的数据是按照从小到大的顺序排列的。如果想按照从大到小的顺序排列数据,则可以在容器排序完成之后,调用 reverse() 算法将容器中的所有数据翻转为逆序即可。例如:
// 将排序完成的容器翻转为逆序,以实现从大到小的排序 reverse(vecScore.begin(), vecScore.end() );sort() 算法在排序过程中,通过“<”关系运算符对数据进行比较,从而确定它们的大小关系进行排序。这就意味着,想要通过 sort() 算法进行排序的数据,必须支持用“<”关系运算符比较大小:
- 对于基本数据类型,例如 int、char、string 等,由于这些数据类型已经重载了“<”关系运算符,具备了使用“<”比较大小的功能,因此 sort() 算法原生就可以对容器中的基本数据类型的数据进行排序,无须进行任何额外工作。
- 如果容器中保存的数据是自定义数据类型,例如某个类的对象或某个结构体的变量等,则需要我们为该类型重载“<”关系运算符。这样,sort() 算法才能使用该运算符来比较容器中两个数据的大小,从而对所有数据进行排序。
例如,容器中保存的是自定义的表示矩形的 Rect 类型对象,我们希望按照矩形的面积对容器中的 Rect 对象进行排序,其代码如下:
// 创建表示矩形的 Rect 类
class Rect
{
public:
Rect() {}; // 默认构造函数
// 构造函数,设定矩形的长和宽
Rect( float fW, float fH )
: m_fW(fW), m_fH(fH) {};
// 重载 "<" 关系运算符,用于比较两个矩形的大小
// 它的参数是另一个 Rect 对象的引用
bool operator < (const Rect& r ) const
{
// 计算两个矩形的面积
float fArea = GetArea(); // 自身的面积
// 另一个矩形的面积
float fAreaOther = r.GetArea();
// 返回两个面积比较的结果作为两个矩形比较的结果
return fArea < fAreaOther;
}
// 获得矩形的面积
float GetArea() const
{
return m_fW * m_fH;
}
// 获得矩形的宽和高
float GetW() const
{
return m_fW;
}
float GetH() const
{
return m_fH;
}
// 获取矩形的周长
float GetGirth() const
{
return (GetW() + GetH()) * 2;
}
// 矩形的属性:长和宽
private:
float m_fW;
float m_fH;
};
// 创建保存 Rect 对象的容器
vector<Rect> vecRect;
// 将多个 Rect 对象添加到容器中
vecRect.push_back( Rect(3, 4) );
vecRect.push_back( Rect(6, 7) );
vecRect.push_back( Rect(8, 1) );
// 对容器中的 Rect 对象进行排序
// 这里使用默认的“<”关系运算符按照面积排序
sort( vecRect.begin(), vecRect.end() );
在这段代码中,我们在 vector 容器中保存的是自定义的 Rect 类的对象。为了使这种数据类型的数据也能够支持 sort() 算法,我们重载了Rect类的“<”关系运算符。该运算符的返回值是 bool 类型,用于表示比较大小的结果;同时它有一个 Rect 引用类型的参数,表示参与比较的另一个 Rect 对象。在这个重载的运算符中,我们具体地定义了两个 Rect 对象比较的规则:首先计算两个矩形的面积,然后将两个面积比较的结果作为两个矩形比较的结果,也就是说,哪个矩形的面积大,就认为这个矩形大。
sort() 算法在对容器中的 Rect 对象进行排序时,会调用这个运算符对两个 Rect 对象进行大小比较,以此决定它们之间的先后顺序。
对容器中的数据进行排序,不仅仅是让数据按照某种顺序排列这么简单,更多时候,我们还会在容器中的数据排序完成后,对数据进行进一步的处理,以获得更多、更丰富的结果。
例如,针对排序完成的容器,可以使用 lower_bound() 算法和 upper_bound() 算法来获得容器中小于某个值或者大于某个值的临界点位置;可以使用 equal_range() 算法获得容器中所有等于某个值的数据范围。
可以说,使用 sort() 算法对容器中的数据进行排序是后续这些算法的前提,而这些算法又扩展了 sort() 算法的结果。两者相互配合使用,可以“优雅”地完成一些常见的数据处理任务。
以前文的学生成绩汇总的例子为例,当使用 sort() 算法对保存在 vecScore 容器中的汇总成绩排序完成后,我们还可以统计所有及格的学生总人数和刚好及格的学生人数,代码如下:
// 汇总学生成绩并排序
// 获取容器中及格分数(大于临界值 59)的临界点
// upper_bound() 算法返回的是指向这个临界点的迭代器
auto itpass =
upper_bound(vecScore.begin(), vecScore.end(), // 容器的数据范围
59); // 临界值
// 获取容器中刚好及格(60)的数据范围
// equal_range() 算法返回的是一个 pair 对象
// 它的 first 成员保存的是这个范围的起始位置
// 而它的 second 成员保存的是这个范围的结束位置
auto passScores = equal_range(vecScore.begin(),
vecScore.end(), // 容器的数据范围
60); // 及格分数
// 输出数据处理的结果
// 输出所有及格的分数
cout<<"所有及格的分数是:"<<endl;
for( auto it = itpass; it != vecScore.end(); ++it )
cout<<*it<<endl;
// 利用迭代器计算符合条件的数据的个数
cout<<"所有及格的学生人数:"<<int(vecScore.end() - itpass)<<endl;
cout<<"刚好及格的学生人数:"<<int(passScores.second - passScores.first)<<endl;
在这里,我们利用 equal_range() 函数返回的迭代器来计算容器中符合条件的数据的数量。然而,这通常不是 equal_range() 函数的主要用途,它更多地用于查找操作。实际上,STL 提供了 count() 算法和 count_if() 算法,它们专门用于统计容器中符合某个条件的数据的数量。使用这两个算法,我们可以以一种更直接和优雅的方式进行计数:
// 统计容器中所有及格的分数个数
// count_if() 算法使用 ispass() 函数判断当前数据是否属于及格分数
// 如果 ispass() 函数返回的是 true,则当前数据属于及格分数,统计在内
int nAllPass = count_if( vecScore.begin(), // 容器数据范围
vecScore.end(), // 判断函数
ispass);
cout<<"所有及格的学生人数:"<<nAllPass<<endl;
// 统计刚好及格的学生人数
// 也就是利用 count() 算法统计容器中有多少个值为 60 的数据
int nPass = count( vecScore.begin(), // 容器数据范围
vecScore.end(), // 被统计的数值
60); // 统计的学生人数
cout<<"刚好及格的学生人数:"<<nPass<<endl;
自定义sort()排序规则
作为 sort() 算法的使用者,我们关心的并不是排序算法的具体实现,更关注的是排序算法的排序规则。在默认情况下,sort() 算法使用“<”关系运算符进行大小比较,并按照从小到大的顺序进行排序。虽然 sort() 算法的这种默认排序方式可以满足大多数需求,但在一些特殊情况下,我们希望按照某些特殊的方式对数据进行排序,即采用自定义的排序规则。
这时,我们就需要用到 sort() 算法的第二个版本,它的原型如下:
template <class RandomAccessIterator, class Compare> void sort ( RandomAccessIterator first, RandomAccessIterator last, Compare comp );从这里可以看到,sort() 算法的第二个版本在第一个版本的基础上增加了一个参数 comp,正是这个增加的参数使我们可以自定义排序规则。
comp 参数可以接受一个函数,该函数用于定义排序的比较规则,因此它也被称为比较函数。比较函数有两个输入参数,它们是要进行比较的数据对应的数据类型,该函数还有一个 bool 类型的返回值。
sort()算法在执行时,会将容器中两个待比较的数据作为实际参数调用这个比较函数进行大小比较。在比较函数中,我们可以自定义比较规则,按照我们需要的方式来比较两个数据的大小,并最终返回一个 bool 值来表示这两个数据的大小关系。sort() 算法会根据这个大小关系来确定它们最终在容器中的先后顺序。
例如,可以利用 sort() 算法中的比较函数重新定义 vecRect 容器中 Rect 对象的排序规则,让它们按照矩形的长进行排序:
// 定义比较函数,实现自己的比较规则
// 比较函数的两个参数的数据类型,就是容器中数据的类型的引用,而返回值类型是 bool 类型
bool sortbyH( const Rect& rect1, const Rect& rect2 )
{
// 在比较函数中,定义具体的比较规则
// 这里比较两个矩形的长,以矩形长的比较结果作为矩形的比较结果
// 默认情况下,数据是按照“<”关系运算符比较后的结果进行排序的
// 所以这里也返回“<”关系运算符比较的结果
return rect1.GetH() < rect2.GetH();
}
// 使用自定义的比较规则代替默认的比较规则对容器中的数据进行排序
sort( vecRect.begin(), vecRect.end(), sortbyH );
在利用 sortbyH() 函数重新定义比较规则,并将它作为 sort() 算法的第三个参数传递给 sort() 算法之后,sort() 算法在排序时会采用我们自定义的比较函数,而不再采用默认的排序规则,即不再使用这个数据类型的“<”关系运算符进行比较。取而代之的事,sort() 算法会调用我们自定义的比较函数来完成对数据的比较。因为可以完全控制比较函数的实现,所以我们可以将特殊的比较规则融入到比较函数中,让 sort() 算法采用我们自定义的比较规则。
自定义比较规则还带来另一个好处,那就是实现比较规则的多样化。例如,如果某天老板心血来潮,希望让 Rect 对象按照矩形的宽进行排序,通过自定义 sort() 算法的比较规则,也能很快实现:
// 定义新的比较函数,实现新的比较规则
bool sortbyW( const Rect& rect1, const Rect& rect2 )
{
return rect1.GetW() < rect2.GetW();
}
// 在 sort() 算法中使用新的比较函数
sort( vecRect.begin(), vecRect.end(), sortbyW );
在这里,我们很快就将新的比较规则运用于比较函数 sortbyW(),然后通过 sort() 算法调用这个比较函数,从而改变了 sort() 算法的比较规则,排序的结果随之发生变化。也就是说,同一个 sort() 算法、不同的比较函数就有不同的比较结果,这大大增加了 sort() 算法的灵活性,如下图所示。
图 1 不同的比较函数,不同的比较结果
一般来说,sort() 算法提供的只是一个排序算法的框架,它负责维护整个排序过程。
例如,从容器中取出两个数据进行比较,并根据比较结果将数据放到容器的合适位置。但是,它将排序算法中最核心、最关键的部分—比较规则的定义,留给了我们。这样,我们可以自定义比较规则,使用相同的固定算法框架,应用不同的自定义比较规则来对不同类型的数据进行排序,从而实现排序算法的通用性和灵活性。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: