单隐层神经网络简介(新手必看)
在每个 epoch(传递训练数据集)中,权重更新过程如下:
此处使用的是批量梯度下降,即计算的梯度是基于整个训练集,同时基于梯度的方向更新模型的权值。其中,定义目标函数为 SSE,记作 J(w)。更进一步,通过将 -J(w) 乘以学习率 η,用以控制下降步伐,从而避免越过代价函数的全局最小值。
基于上述优化方式,更新所有的权重系数,定义每个权重的偏导数如下:
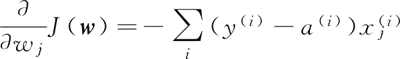
其中,y(i) 为特定样本 x(i) 的类别标签,a(i) 代表的是神经元的激活函数,在自适应神经元中是一个线性函数:
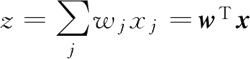
使用激活函数计算梯度更新,进一步实现一个阈值函数,将连续值输出压缩成二进制类别标签:
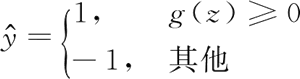
下图为单隐层神经网络的结构:
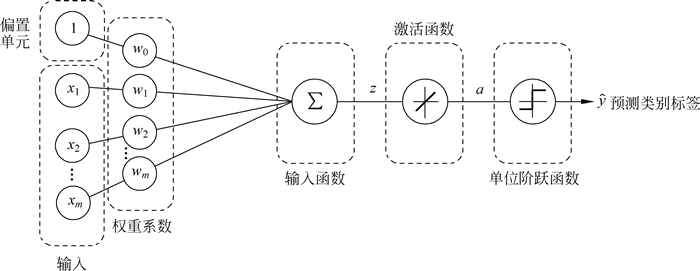
图 4 单隐层神经网络的结构
如上图所示,因为输入层和输出层之间仅仅有一条链路,所以称其为单层网络。另一种加速模型学习的优化方式为随机梯度下降(Stochastic Gradient Descent,SGD),SGD 近似于单个训练样本,或近似于使用一小部分训练样本即小批量学习。
SGD 由于权重更新更加频繁,相较于批量梯度下降,其学习速度更快。同时噪声特性也使 SGD 在训练时具有非线性激活函数。此处引入的噪声可以促进优化目标,避免陷入局部最小。
w=w+Δw其中,Δw=-η▽J(w)。
此处使用的是批量梯度下降,即计算的梯度是基于整个训练集,同时基于梯度的方向更新模型的权值。其中,定义目标函数为 SSE,记作 J(w)。更进一步,通过将 -J(w) 乘以学习率 η,用以控制下降步伐,从而避免越过代价函数的全局最小值。
基于上述优化方式,更新所有的权重系数,定义每个权重的偏导数如下:
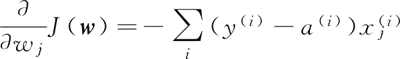
其中,y(i) 为特定样本 x(i) 的类别标签,a(i) 代表的是神经元的激活函数,在自适应神经元中是一个线性函数:
ϕ(z)=z=a其中,z 为连接输入层和输出层的权值线性组合:
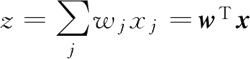
使用激活函数计算梯度更新,进一步实现一个阈值函数,将连续值输出压缩成二进制类别标签:
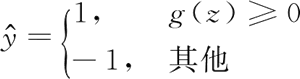
下图为单隐层神经网络的结构:

图 4 单隐层神经网络的结构
如上图所示,因为输入层和输出层之间仅仅有一条链路,所以称其为单层网络。另一种加速模型学习的优化方式为随机梯度下降(Stochastic Gradient Descent,SGD),SGD 近似于单个训练样本,或近似于使用一小部分训练样本即小批量学习。
SGD 由于权重更新更加频繁,相较于批量梯度下降,其学习速度更快。同时噪声特性也使 SGD 在训练时具有非线性激活函数。此处引入的噪声可以促进优化目标,避免陷入局部最小。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: