C#递归函数详解(附带实例)
一个函数调用本身的动作,称为递归的调用。递归函数调用有下列特性:
递归函数可以使程序本身变得很简洁,但是设计这类程序时如果不小心,就很容易掉入无限递归的陷阱中,所以使用这类函数时,一定要特别小心。
例如,设计一个递归函数,因为这个函数没有终止条件,所以其会变成一个无限循环,这个程序会一直输出 5, 4, 3, …。为了让读者看到输出结果,这个程序会每隔 1 秒输出一次数字。
执行结果为:
再看一个例子,设计递归函数输出 1, 2, …, 5 的结果。
这个程序第 1 次进入 Recur() 函数时,因为 i 等于 5,所以会先执行第 6 行 Recur(i-1),这时会将尚未执行的第 7 行 Console.Write() 推入 (push) 栈。
第 2 次进入 Recur() 函数时,因为 i 等于 4,所以会先执行第 6 行 Recur(i-1),这时会将尚未执行的第 7~第 8 行 Console.Write() 和 return 0 推入栈。其他以此类推,所以可以得到下图:
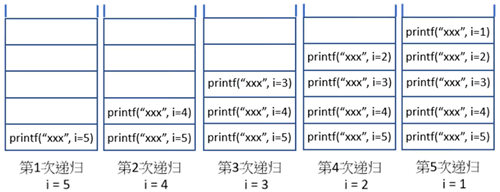
这个程序第 6 次进入 Recur() 函数时,i 等于 0,因为 i<1 时会执行第 7 行 return 0,这时函数会终止。接着函数会将存储在栈的指令一一取出执行,执行时后进先出 (last in first out),也就是从上往下取出执行,整个说明图如下所示。
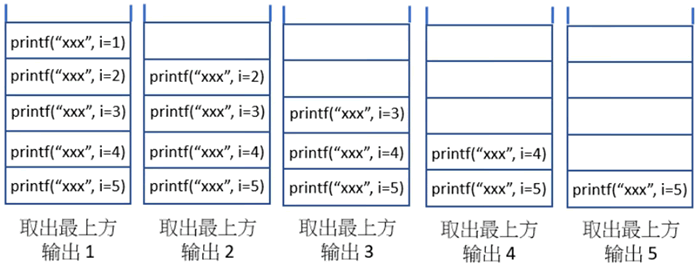
上图由左到右,可以得到 1, 2, …, 5 的输出。下一个实例是计算累加总和的,比上述实例稍微复杂,读者可以逐步推导,累加的基本概念如下:
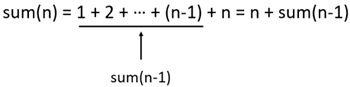
将上述概念转成递归公式如下:
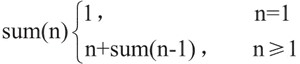
使用递归函数计算 1+2+…+5 的值:
在数学中,正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,假设进行 n 的阶乘,则表达式如下:
例如,列出 5 的阶乘的结果:
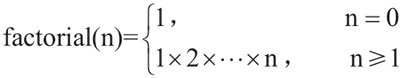
设计非递归的阶乘函数,计算当 n=5 时的值:
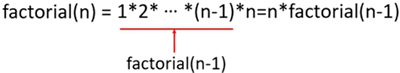
有了上述概念后,可以将阶乘公式改成下列公式:
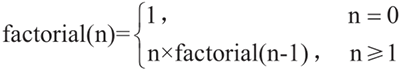
上述公式每一次传递 fcatorial(n-1),都会将问题范围变小,这就是递归的概念。
设计递归的阶乘函数:
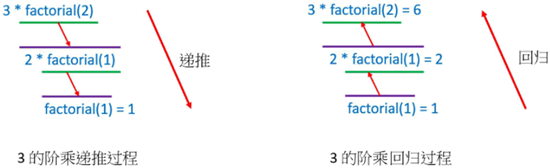
在编译程序是使用栈处理上述递归调用,这是一种后进先出的数据结构,下图是编译程序实际使用栈方式使用内存的情形:
在计算机术语中将数据放入栈的动作称为推入。上述 3 的阶乘中,编译程序实际回归处理过程,其实就是将数据从栈中取出,此动作在计算机术语中称为取出,整个概念如下所示:
阶乘数的概念,最常应用的是业务员旅行问题。业务员旅行是算法里面一个非常著名的问题,许多人在思考业务员如何从拜访不同城市的路线中,找出最短的拜访路径,下列将逐步分析。
假设有新竹、竹东,两个城市,拜访方式有两个选择:

假设现在多了一个城市竹北,从竹北出发,从两个城市可以知道有两条路径。从新竹或竹东出发也可以有 2 条路径,所以可以有 6 种拜访方式:
如果再细想,两个城市的拜访路径有两种,3 个城市的拜访路径有 6 种,其实符合阶乘公式:
比 3 个城市多了一个城市,所以拜访路径选择总数如下:
- 递归函数在每次处理时,都会使问题的范围缩小。
- 必须有一个终止条件来结束递归函数。
递归函数可以使程序本身变得很简洁,但是设计这类程序时如果不小心,就很容易掉入无限递归的陷阱中,所以使用这类函数时,一定要特别小心。
从掉入无限递归说起
前面讲一个函数可以调用自己,这个动作称为递归,设计递归最容易掉入无限递归的陷阱。例如,设计一个递归函数,因为这个函数没有终止条件,所以其会变成一个无限循环,这个程序会一直输出 5, 4, 3, …。为了让读者看到输出结果,这个程序会每隔 1 秒输出一次数字。
int Recur(int i)
{
Console.Write($"{i} ");
Thread.Sleep(1000); // 休息 1 秒
return Recur(i - 1);
}
Recur(5);
执行结果为:
5 4 3 2 1 0 -1 -2 ......
上述第 5 行虽然使用 Recur(i-1),让数字范围缩小了,但是最大的问题是没有终止条件,所以造成了无限递归。为此,我们在设计递归时需要使用 if 条件语句来注明终止条件:
int Recur(int i)
{
Console.Write($"{i} ");
Thread.Sleep(1000);
if (i <= 1) // 结束条件
return 0;
else
return Recur(i - 1); // 每次调用让自己减 1
}
Recur(5);
这是最简单的递归函数,列出 5, 4, …, 1 的数列作为结果,这个问题很清楚了,结束条件是 1,所以可以在 Recur() 函数内撰写结束条件。执行结果为:
5 4 3 2 1
上述当第 8 行 Recur(i-1),当参数是 i-1 是 1 时,会执行 return 0,所以递归条件就结束了。再看一个例子,设计递归函数输出 1, 2, …, 5 的结果。
int Recur(int i)
{
if (i < 1) // 结束条件
return 0;
else
Recur(i - 1); // 每次调用让自己减 1
Console.Write($"{i} ");
return 0;
}
Recur(5);
执行结果为:
1 2 3 4 5
C# 语言或其他有递归功能的程序语言,一般是采用栈方式来存储递归期间尚未执行的指令,所以上述程序在每一次递归期间都会将第 7 行先存储在栈中,一直到递归结束,再一一取出栈的数据执行。这个程序第 1 次进入 Recur() 函数时,因为 i 等于 5,所以会先执行第 6 行 Recur(i-1),这时会将尚未执行的第 7 行 Console.Write() 推入 (push) 栈。
第 2 次进入 Recur() 函数时,因为 i 等于 4,所以会先执行第 6 行 Recur(i-1),这时会将尚未执行的第 7~第 8 行 Console.Write() 和 return 0 推入栈。其他以此类推,所以可以得到下图:

这个程序第 6 次进入 Recur() 函数时,i 等于 0,因为 i<1 时会执行第 7 行 return 0,这时函数会终止。接着函数会将存储在栈的指令一一取出执行,执行时后进先出 (last in first out),也就是从上往下取出执行,整个说明图如下所示。

上图由左到右,可以得到 1, 2, …, 5 的输出。下一个实例是计算累加总和的,比上述实例稍微复杂,读者可以逐步推导,累加的基本概念如下:
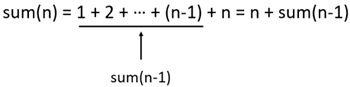
将上述概念转成递归公式如下:
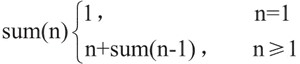
使用递归函数计算 1+2+…+5 的值:
int Recur(int i)
{
if (i < 1) // 结束条件
return 0;
else
Recur(i - 1); // 每次调用让自己减 1
Console.Write($"{i} ");
return 0;
}
Recur(5);
执行结果为:
total = 15
非递归设计阶乘数函数
阶乘数(factorial)概念是由法国数学家克里斯蒂安·克兰普(Christian Kramp, 1760—1826)发表的,他学医但同时对数学感兴趣,发表了许多数学文章。在数学中,正整数的阶乘(factorial)是所有小于及等于该数的正整数的积,假设进行 n 的阶乘,则表达式如下:
n!
同时也定义 0 和 1 的阶乘是 1。
0! = 1
1! = 1
例如,列出 5 的阶乘的结果:
5! = 5 * 4 * 3 * 2 * 1 = 120
我们可以使用下列式子来定义阶乘公式: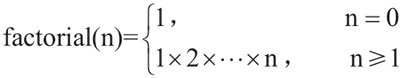
设计非递归的阶乘函数,计算当 n=5 时的值:
int Factorial(int n)
{
int fact = 1;
int i;
for (i = 1; i <= n; i++)
{
fact *= i;
Console.WriteLine($"{i}! = {fact}");
}
return fact;
}
Console.WriteLine($"Factorial(5) = {Factorial(5)}");
执行结果为:
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
Factorial(5) = 120
从一般函数进化到递归函数
针对阶乘数 n ≥ 1 的情况,我们可以将阶乘数用下列公式表示: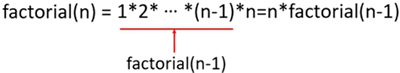
有了上述概念后,可以将阶乘公式改成下列公式:
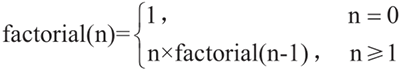
上述公式每一次传递 fcatorial(n-1),都会将问题范围变小,这就是递归的概念。
设计递归的阶乘函数:
int Factriol(int n)
{
int fact;
if (n == 0) // 终止条件
fact = 1;
else
fact = n * Factriol(n - 1); // 递归调用
return fact;
}
int x = 3;
Console.WriteLine($"{x}! = {Factriol(x)}");
x = 5;
Console.WriteLine($"{x}! = {Factriol(x)}");
执行结果为:
3! = 6
5! = 120

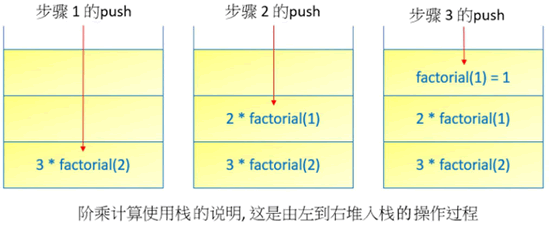
在编译程序是使用栈处理上述递归调用,这是一种后进先出的数据结构,下图是编译程序实际使用栈方式使用内存的情形:

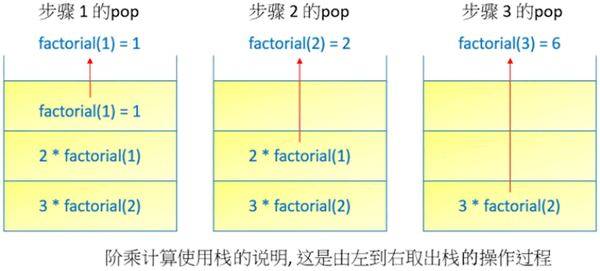
在计算机术语中将数据放入栈的动作称为推入。上述 3 的阶乘中,编译程序实际回归处理过程,其实就是将数据从栈中取出,此动作在计算机术语中称为取出,整个概念如下所示:

阶乘数的概念,最常应用的是业务员旅行问题。业务员旅行是算法里面一个非常著名的问题,许多人在思考业务员如何从拜访不同城市的路线中,找出最短的拜访路径,下列将逐步分析。
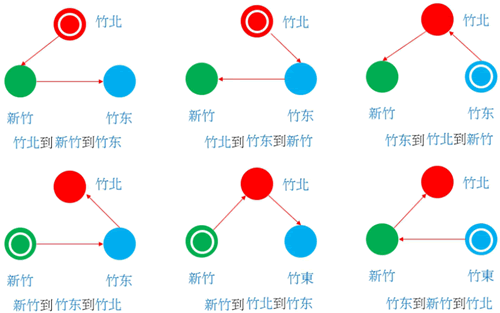
假设有新竹、竹东,两个城市,拜访方式有两个选择:

假设现在多了一个城市竹北,从竹北出发,从两个城市可以知道有两条路径。从新竹或竹东出发也可以有 2 条路径,所以可以有 6 种拜访方式:

如果再细想,两个城市的拜访路径有两种,3 个城市的拜访路径有 6 种,其实符合阶乘公式:
2!=1*2=2
3!=1*2*3=6
比 3 个城市多了一个城市,所以拜访路径选择总数如下:
4!=1*2*3*4=24
其总共有 24 条拜访路径,如果有 5 个或 6 个城市要拜访,拜访路径选择总数如下:
5!=1*2*3*4*5=120
6!=1*2*3*4*5*6=720
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: