BF模式匹配算法(Java实现)
串的模式匹配也称为子串的定位操作,即查找子串在主串中出现的位置。
设有主串 S 和子串 T,若在主串 S 中找到一个与子串 T 相等的串,则返回串 T 的第一个字符在串 S 中的位置。其中,主串 S 又称为目标串,子串 T 又称为模式串。
BF(Brute-Force)算法的思想是从主串 S="s0s1…sn-1" 的第 pos 个字符开始与模式串 T="t0t1…tm-1" 的第一个字符比较,若相等,则继续逐个比较后续字符,否则从主串的下一个字符开始重新与模式串 T 的第一个字符比较,以此类推。
若在主串 S 中存在与模式串 T 相等的连续字符序列,则匹配成功,函数返回模式串 T 中第一个字符在主串 S 中的位置,否则函数返回 -1 表示匹配失败。
例如,主串 S="abaababaddecab",子串 T="abad",S 的长度为 n=13,T 的长度为 m=4。用变量 i 表示主串 S 中当前正在比较的字符的下标,变量 j 表示子串T中当前正在比较的字符的下标。模式匹配的过程如下图所示:
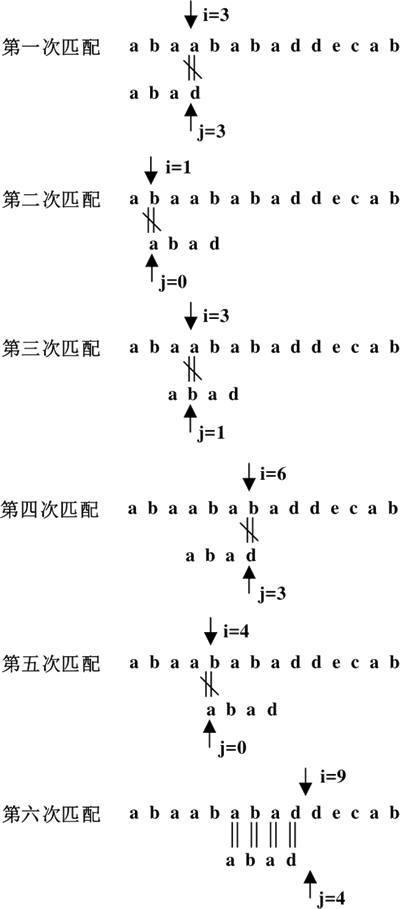
图 1 Brute-Force模式的匹配过程
假设串采用顺序存储方式存储,则 BF 匹配算法如下:
然而,在有些情况下,该算法的效率却很低。例如设主串 S="aaaaaaaaaaaaab",模式串 T="aaab"。其中,n=14,m=4。因为模式串的前 3 个字符是"aaa",主串的前 13 个字符是 "aaaaaaaaaaaaa",每趟比较模式串的最后一个字符与主串中的字符不相等,所以均需要将主串的指针回退,从主串的下一个字符开始与模式串的第一个字符重新比较。在整个匹配过程中,主串的指针需要回退 9 次,匹配不成功的比较次数是 10×4,成功匹配的比较次数是 4 次,因此总的比较次数是 10×4+4=11×4,即 (n-m+1)m。
可见,BF 匹配算法在最好的情况下,主串的前 m 个字符刚好与模式串相等,时间复杂度为
在 BF 算法中,即使主串与模式串已有多个字符经过比较相等,只要有一个字符不相等,就需要将主串的比较位置回退。
设有主串 S 和子串 T,若在主串 S 中找到一个与子串 T 相等的串,则返回串 T 的第一个字符在串 S 中的位置。其中,主串 S 又称为目标串,子串 T 又称为模式串。
BF(Brute-Force)算法的思想是从主串 S="s0s1…sn-1" 的第 pos 个字符开始与模式串 T="t0t1…tm-1" 的第一个字符比较,若相等,则继续逐个比较后续字符,否则从主串的下一个字符开始重新与模式串 T 的第一个字符比较,以此类推。
若在主串 S 中存在与模式串 T 相等的连续字符序列,则匹配成功,函数返回模式串 T 中第一个字符在主串 S 中的位置,否则函数返回 -1 表示匹配失败。
例如,主串 S="abaababaddecab",子串 T="abad",S 的长度为 n=13,T 的长度为 m=4。用变量 i 表示主串 S 中当前正在比较的字符的下标,变量 j 表示子串T中当前正在比较的字符的下标。模式匹配的过程如下图所示:

图 1 Brute-Force模式的匹配过程
假设串采用顺序存储方式存储,则 BF 匹配算法如下:
public int B_FIndex(SeqString S, SeqString T, int pos) {
// 从主串 S 的第 pos 个位置开始查找模式串 T,若找到,则返回子串在主串的位置;否则返回-1
int i = pos - 1;
int j = 0;
count = 0;
while (i < S.length && j < T.length) {
if (S.str[i] == T.str[j]) { // 若串 S 和串 T 中的对应位置字符相等,则继续比较下一个字符
i += 1;
j += 1;
} else { // 若当前对应位置的字符不相等,则从串 S 的下一个字符开始,T 的第 0 个字符开始比较
i = i - j + 1;
j = 0;
}
count++;
}
if (j >= T.length) // 若在 S 中找到串 T,则返回子串 T 在主串 S 的位置
return i - j + 1;
else
return -1;
}
BF 匹配算法简单且容易理解,并且进行某些文本处理时,效率也比较高,如检查 " Welcome" 是否存在于主串 "Nanjing University is a comprehensive university with a long history. Welcome to Nanjing University." 中时,上述算法中 while 循环次数(进行单个字符比较的次数)为 79(70+1+8),除了遇到主串中呈黑体的 "w" 字符,需要比较两次外,其他每个字符均只和模式串比较了一次。在这种情况下,此算法的时间复杂度为 O(n+m)。其中,n 和 m 分别为主串和模式串的长度。然而,在有些情况下,该算法的效率却很低。例如设主串 S="aaaaaaaaaaaaab",模式串 T="aaab"。其中,n=14,m=4。因为模式串的前 3 个字符是"aaa",主串的前 13 个字符是 "aaaaaaaaaaaaa",每趟比较模式串的最后一个字符与主串中的字符不相等,所以均需要将主串的指针回退,从主串的下一个字符开始与模式串的第一个字符重新比较。在整个匹配过程中,主串的指针需要回退 9 次,匹配不成功的比较次数是 10×4,成功匹配的比较次数是 4 次,因此总的比较次数是 10×4+4=11×4,即 (n-m+1)m。
可见,BF 匹配算法在最好的情况下,主串的前 m 个字符刚好与模式串相等,时间复杂度为
O(m);在最坏的情况下,BF匹配算法的时间复杂度是 O(n*m)。在 BF 算法中,即使主串与模式串已有多个字符经过比较相等,只要有一个字符不相等,就需要将主串的比较位置回退。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: